PEARL Model Overview
The PEARL (ProjEcting Age, multmoRbidity, and poLypharmacy) model is an agent-based simulation model of HIV care in the United States. The model leverages the power of the North American AIDS Cohort Collaboration on Research and Design (NA-ACCORD) data set. Data on ~200,000 HIV-infected individuals are provided by over 200 sites across North America. This size of this dataset allows us to treat 15 sub-populations independently. The PEARL model characterizes population by sex (male and female), race (white, black, and Hispanic), and risk (men who have sex with men, intravenous drug users, and heterosexual HIV risk).
Table 1: Sub-Populations Used in the PEARL Model
| Population | Race | Risk | Sex | Code |
|---|---|---|---|---|
| Black Heterosexual Women | Black | HET | Female | het_black_female |
| Black Heterosexual Men | Black | HET | Male | het_black_male |
| Hispanic Heterosexual Women | Hispanic | HET | Female | het_hisp_female |
| Hispanic Heterosexual Men | Hispanic | HET | Male | het_hisp_male |
| White Heterosexual Women | White | HET | Female | het_white_female |
| White Heterosexual Men | White | HET | Male | het_white_male |
| Black Women Who Use Intravenous Drugs | Black | IDU | Female | idu_black_female |
| Black Men Who Use Intravenous Drugs | Black | IDU | Male | idu_black_male |
| Hispanic Women Who Use Intravenous Drugs | Hispanic | IDU | Female | idu_hisp_female |
| Hispanic Men Who Use Intravenous Drugs | Hispanic | IDU | Male | idu_hisp_male |
| White Women Who Use Intravenous Drugs | White | IDU | Female | idu_white_female |
| White Men Who Use Intravenous Drugs | White | IDU | Male | idu_white_male |
| Black Men Who Have Sex With Men | Black | MSM | Male | msm_black_male |
| Hispanic Men Who Have Sex With Men | Hispanic | MSM | Male | msm_hisp_male |
| White Men Who Have Sex With Men | White | MSM | Male | msm_white_male |
The PEARL model runs in discrete time steps representing one year. The simulations begin in year 2009 by creating an initial population of HIV-infected individuals receiving or disengaged from ART in the US. The size of this population and the distribution of their ages, ART initiation years, and CD4 count at ART initiation is estimated based on data available from NA-ACCORD and the Centers for Disease Control and Prevention (CDC). At the beginning of each simulated year (2010 – 2030), a population of those newly diagnosed with HIV enter the model, and a specific proportion (modeled as an increasing function of time) of these individuals link to HIV care and start ART. The population size, age, and CD4 count distributions at ART initiation are estimated from CDC’s and NA-ACCORD’s data. Individuals on ART experience a likelihood of mortality and disengagement from care over time. Upon disengagement, individuals experience an increase in probability of mortality and a gradual reduction in CD4 count. Time-varying CD4 count is updated for all individuals in the model depending on their HIV care status (i.e., increasing among those in care and decreasing among those out of care). All simulation parameters have been estimated from CDC’s and NA-ACCORD’s data for year 2010 to 2017. Simulated outcomes, in terms of age distribution of population in HIV care, are cross-validated against NA-ACCORD’s data during this period. Model projections are made from year 2018 to 2030.
Clarification on terminology: Given the complexities involved in defining, parametrizing and calibrating all steps of the HIV care continuum for the 15 sub-groups, we have limited the scope of the PEARL model to population of HIV infected individuals who have ever been and/or are currently on ART. Following this definition, the simulated population is divided into two groups including “ART users” (those currently on ART) and “ART non-users” (those previously on ART who disengaged from treatment and are currently off ART). Furthermore, the usage of term “HIV care” in this text is closely related to previous or current instances of “ART usage”, and does not include prior steps to ART initiation such as diagnosed, linked to care, retained, etc. We further underscore the difference in terminology used to refer to “population on ART” (those receiving ART in a given period of time, aka ART users), and “population initiating ART” (those starting ART for the first time, aka first time ART initiators) throughout the text.
Initial Population in Year 2009
Population Size
The size of the initial sub-populations in using ART in 2009 is estimated from CDC surveillance data through the Medical Monitoring Project (MMP).
First, the estimated number of persons living with HIV infection in 2009 for each sex and risk group combination is taken from table 14a in the 2013 HIV Surveillance Report. We then use table 17a in the 2010 HIV Surveillance Report to calculate the proportion of each risk/sex group by race. We multiply these two numbers to get an estimate of the total number of persons in each sub-population who are living with HIV.
Finally, we multiply the estimated number living with HIV by estimated proportion of that sub-population to be receiving ART treatment. These estimates come from different sources depending on the sub-population.
Table 2: Total ART Users in 2009
| Population | # With HIV Per Risk/Sex | Proportion By Race | # By Sub-Population | Proportion On ART | Total On ART In 2009 | ART Source |
|---|---|---|---|---|---|---|
| het_black_female | 148,349 | 0.613 | 90,981 | 0.514 | 46,764 | CDC MMWR, February 7, 2014, Table 3 |
| het_black_male | 65,857 | 0.632 | 41,608 | 0.421 | 17,516 | CDC MMWR, February 7, 2014, Table 3 |
| het_hisp_female | 148,349 | 0.191 | 28,342 | 0.498 | 14,114 | CDC MMWR, October 10, 2014, Table 3 |
| het_hisp_male | 65,857 | 0.212 | 13,940 | 0.459 | 6,398 | CDC MMWR, October 10, 2014, Table 3 |
| het_white_female | 148,349 | 0.167 | 24,742 | 0.551 | 13,632 | Correspondence with Luke Shouse, CDC |
| het_white_male | 65,857 | 0.131 | 8,635 | 0.37 | 3,194 | Correspondence with Luke Shouse, CDC |
| idu_black_female | 53,717 | 0.528 | 28,350 | 0.498 | 14,118 | CDC MMWR, February 7, 2014, Table 3 |
| idu_black_male | 134,962 | 0.429 | 57,881 | 0.34 | 19,679 | CDC MMWR, February 7, 2014, Table 3 |
| idu_hisp_female | 53,717 | 0.199 | 10,711 | 0.341 | 3,652 | CDC MMWR, October 10, 2014, Table 3 |
| idu_hisp_male | 134,962 | 0.270 | 36,391 | 0.31 | 11,281 | CDC MMWR, October 10, 2014, Table 3 |
| idu_white_female | 53,717 | 0.245 | 13,152 | 0.55 | 7,233 | Correspondence with Luke Shouse, CDC |
| idu_white_male | 134,962 | 0.275 | 37,145 | 0.455 | 16,900 | Correspondence with Luke Shouse, CDC |
| msm_black_male | 414,232 | 0.293 | 12,1240 | 0.471 | 57,104 | CDC MMWR, September 26, 2014, Table 3 |
| msm_hisp_male | 414,232 | 0.201 | 83,125 | 0.492 | 40,897 | CDC MMWR, September 26, 2014, Table 3 |
| msm_white_male | 414,232 | 0.474 | 196,500 | 0.496 | 97,464 | CDC MMWR, September 26, 2014, Table 3 |
Age Distribution
The age distribution of each sub-population was modeled using a two-component mixed normal distribution (resulting in the best fit among alternative models), as follows:
\[f(x|\lambda_1, \mu_1, \sigma_1, \mu_2, \sigma_2) = \lambda_1 g(x|\mu_1, \sigma_1) + (1 - \lambda_1)g(x|\mu_2, \sigma_2)\]where
\[g(x|\mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]is just the normal distribution. Here $x$ is age of those on ART in year 2009, $\lambda_1$ is the mixing proportion, and the $\mu$’s and $\sigma$’s are the means and standard deviations of the bimodal distribution. These parameters (Table 3) were obtained by fitting to the NA-ACCORD population of ART users in 2009. The normalmixEM2comp function of the mixtools package for R was used to fit the distributions. When initializing a simulation run, the ages of the 2009 population were drawn from a distribution with the same parameters after being truncated at ages 18 and 85.
Table 3: Coefficients for Age of Initial Population
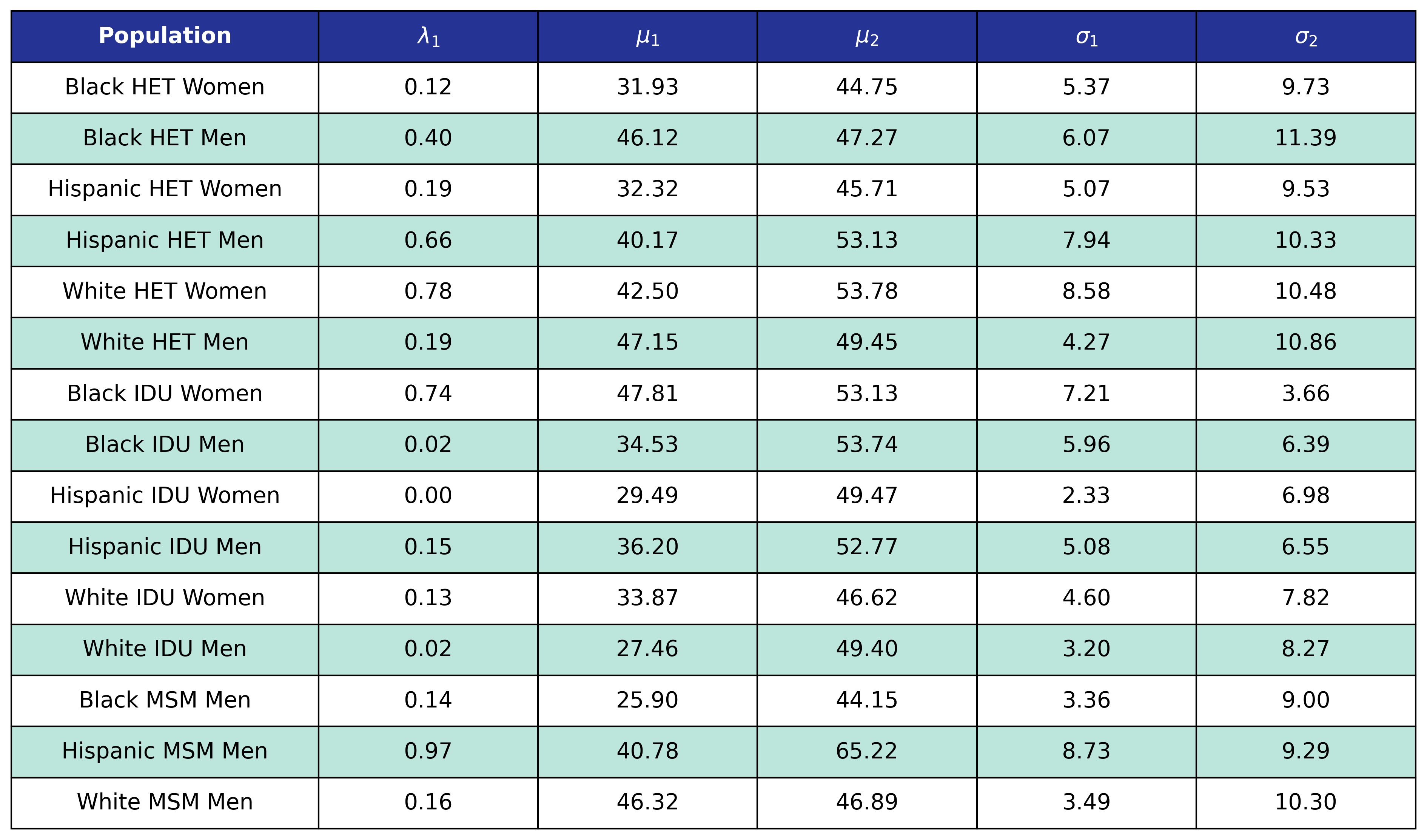
Figure 1a: HET Female
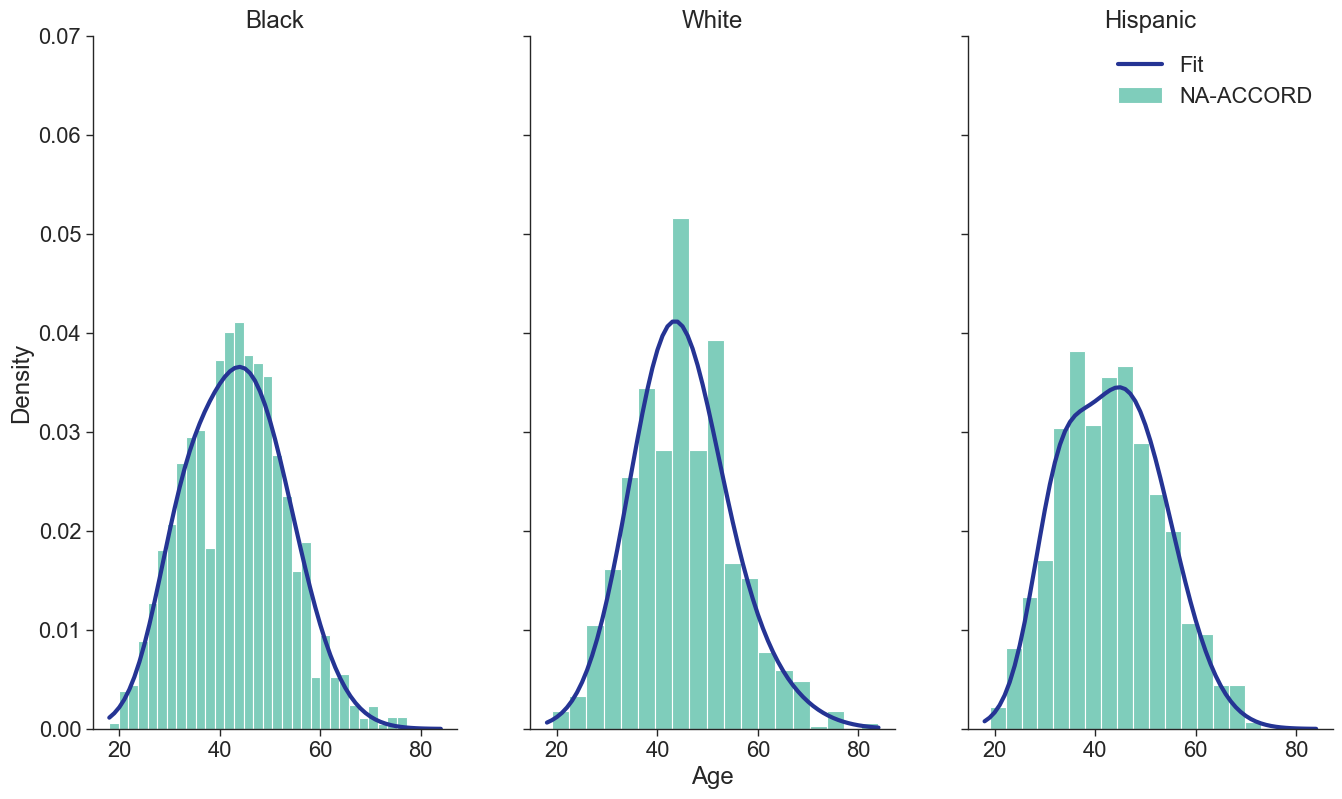
Figure 1b: HET Male
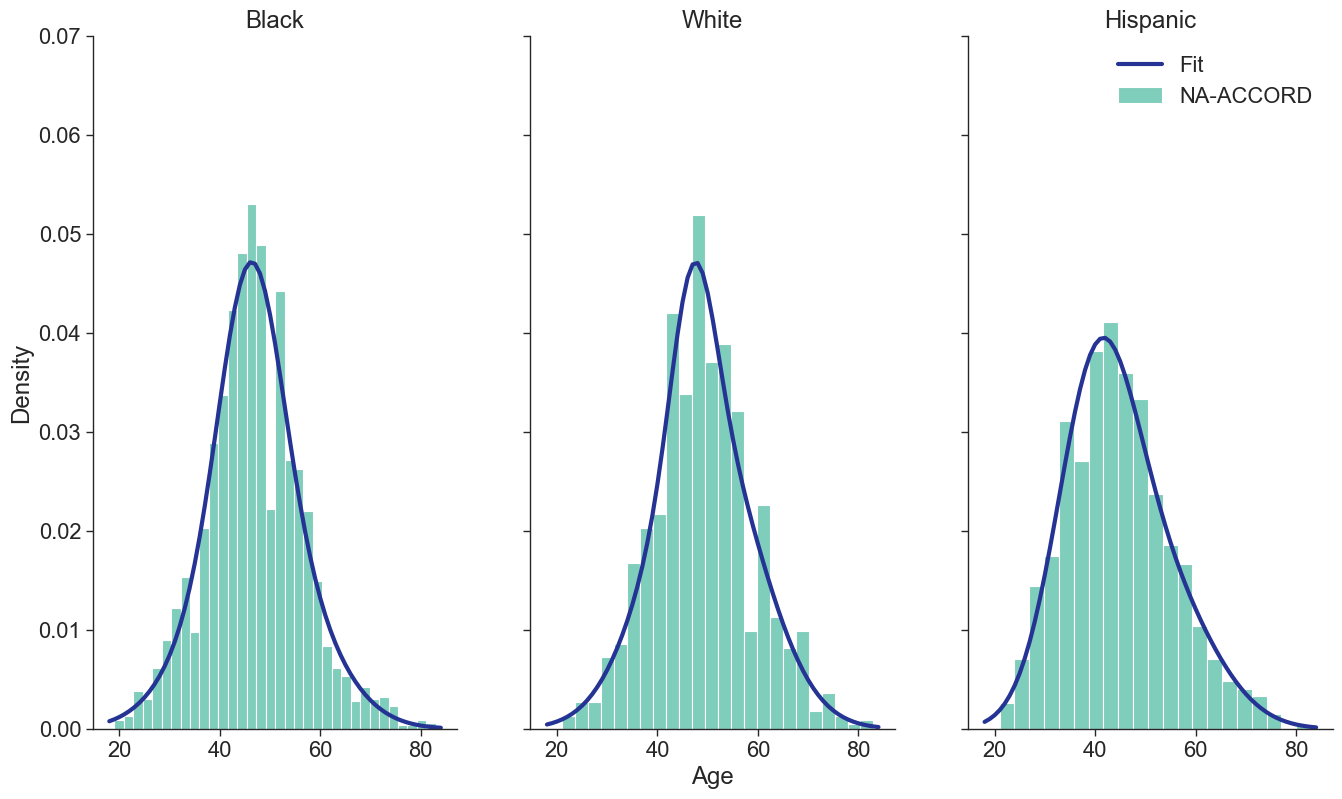
Figure 1c: IDU Female
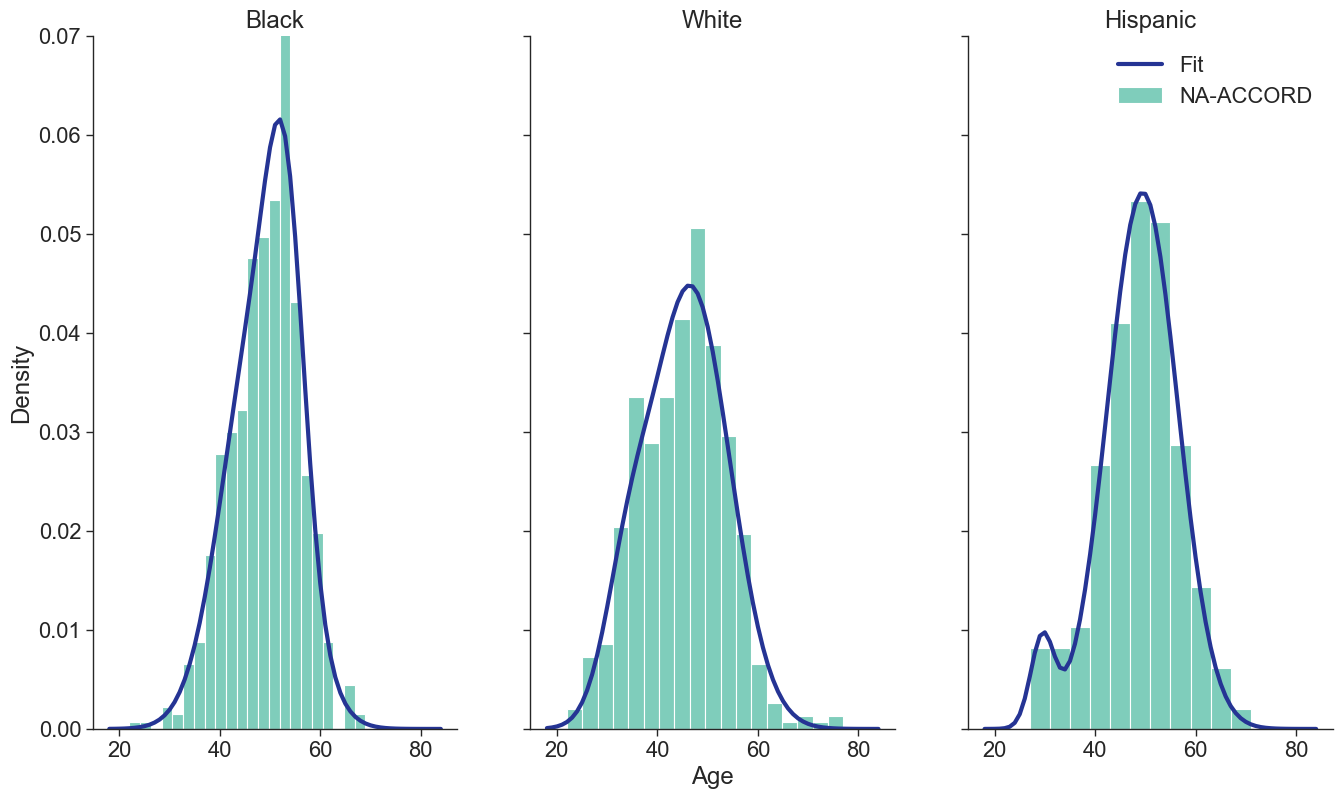
Figure 1d: IDU Male
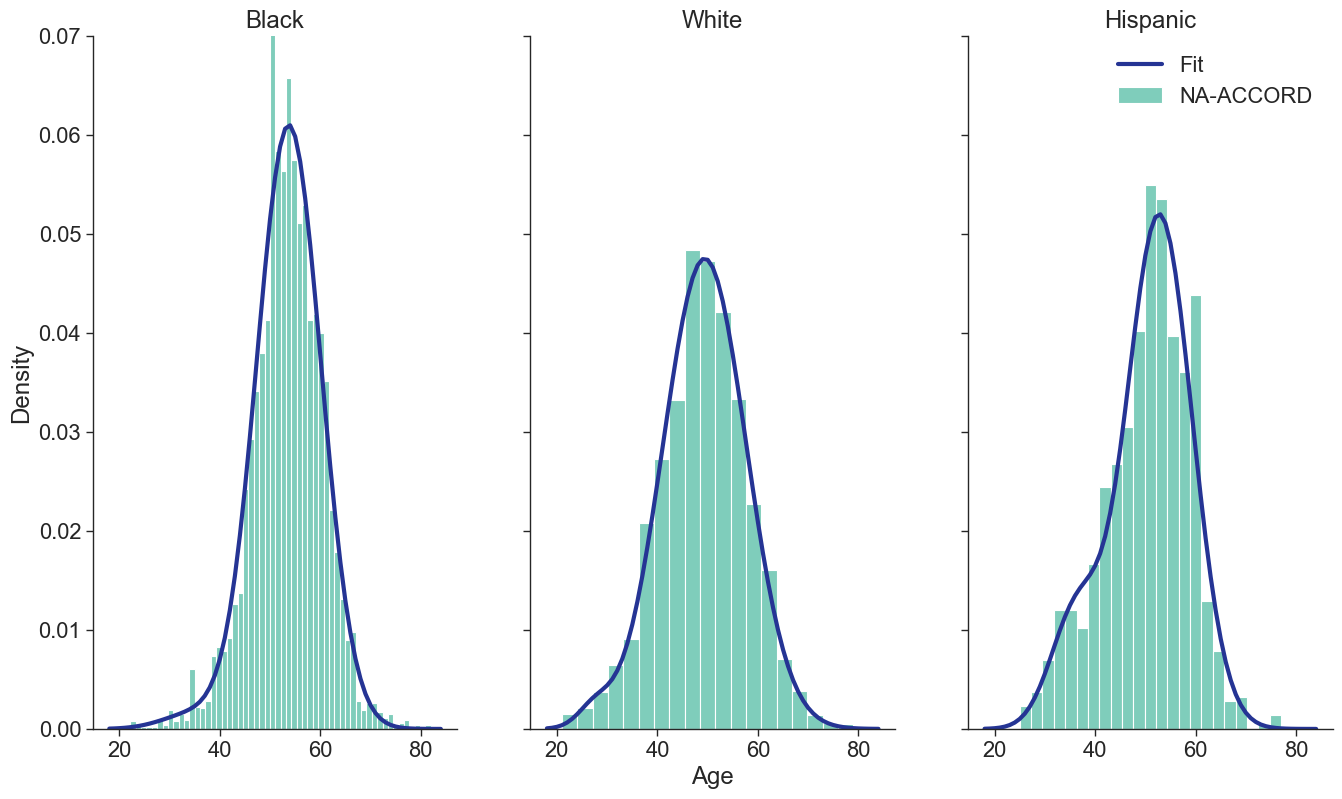
Figure 1e: MSM
Year of ART Initiation
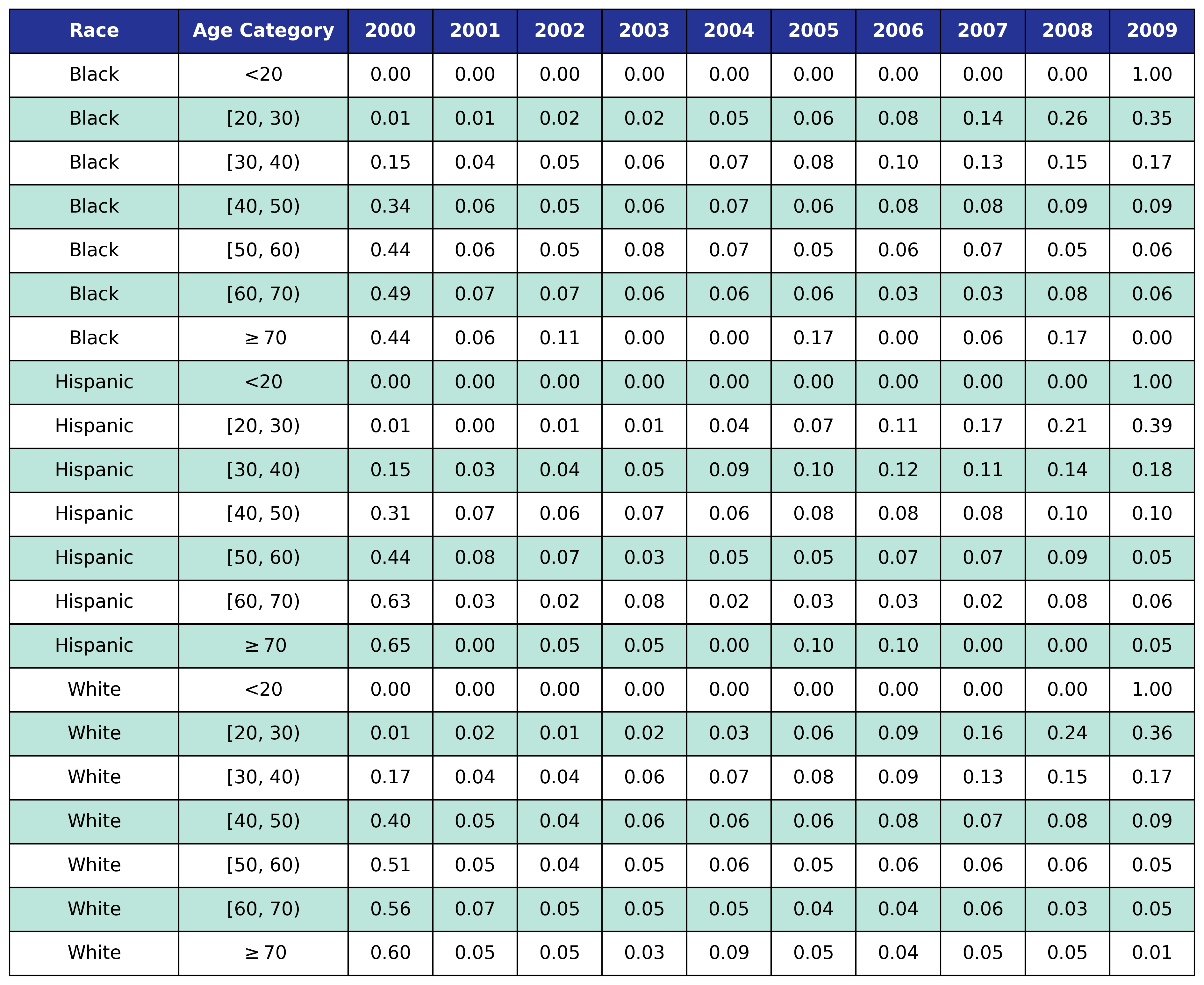
To estimate the original year of ART initiation among the simulated population, we applied available data from the NA-ACCORD population on ART in year 2009. To this end, each sub-population was broken into the seven age categories, including <20, [20,30), [30,40), [40,50), [50,60), [60,70), $\geq$70. Within each category, we then estimated the proportion initiating ART in each year between 2000 and 2009 as shown in Table 4. Those initiating ART prior to 2000 were counted in the 2000 category. If there were no data from a given population in a certain age category, the proportions from the white MSM population were used as indicated by dashes in the following tables. We use the 2009 NA-ACCORD population to inform the ART initiation year of our starting population.
Table 4a: HET Female
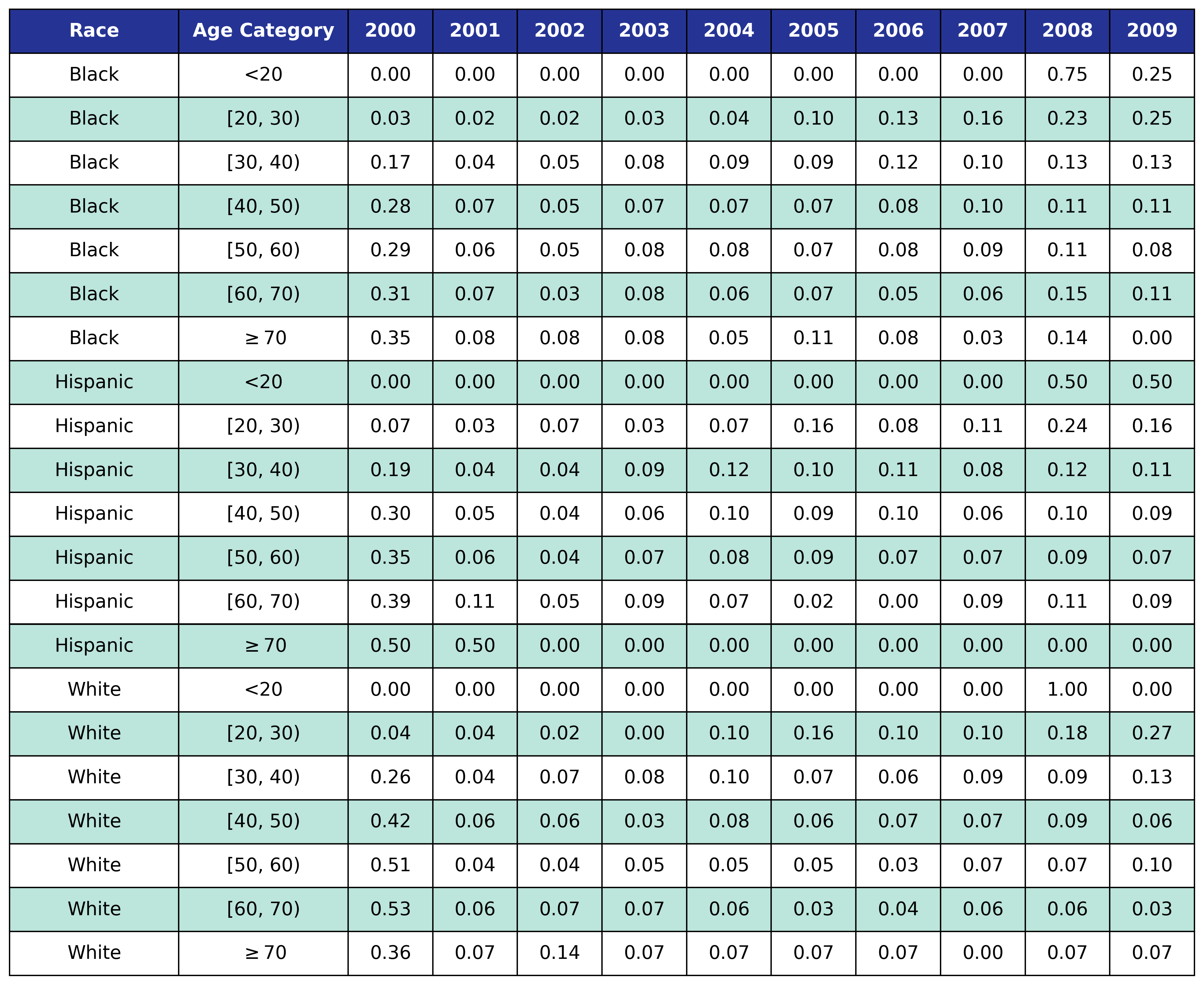
Table 4b: HET Male
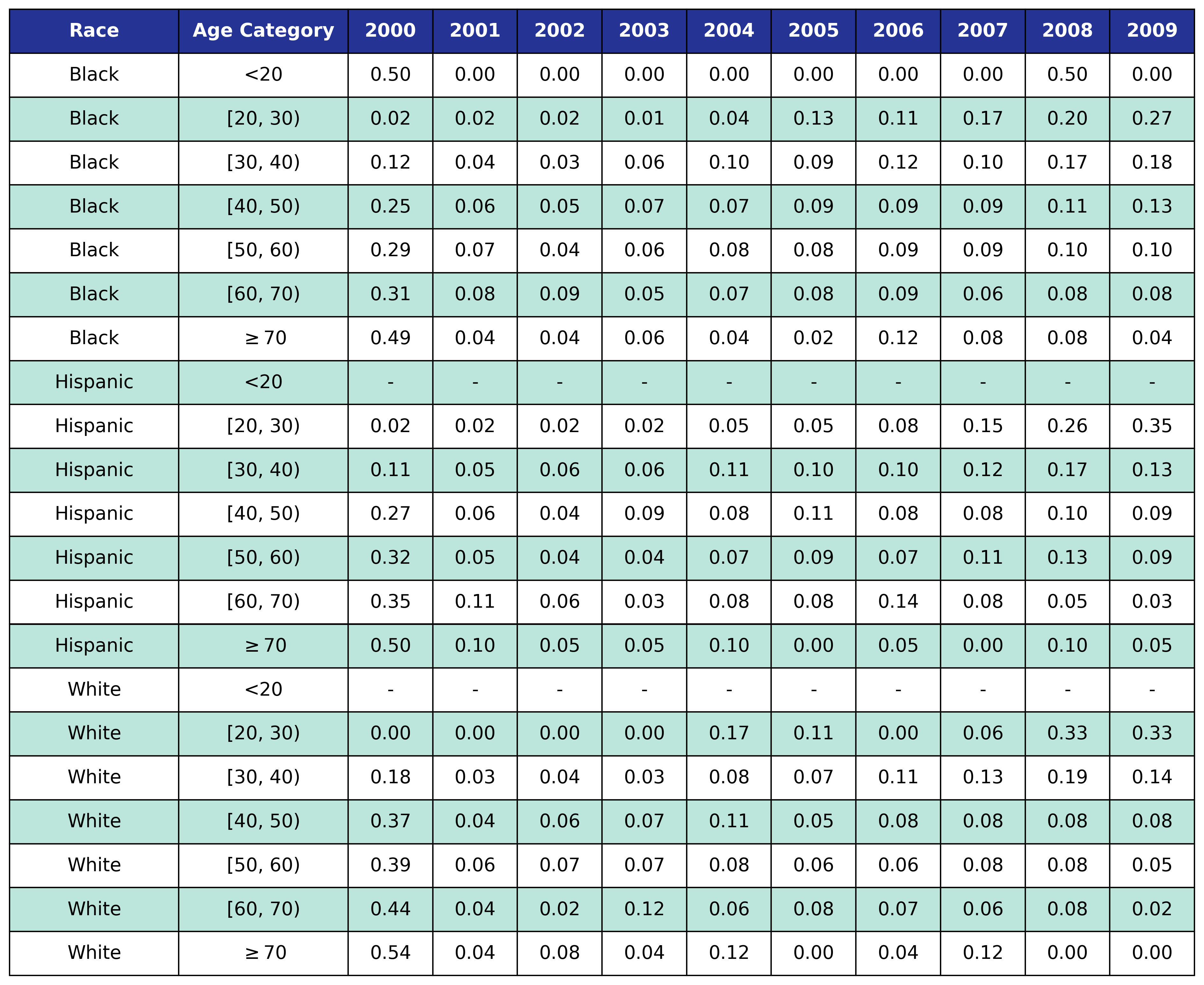
Table 4c: IDU Female
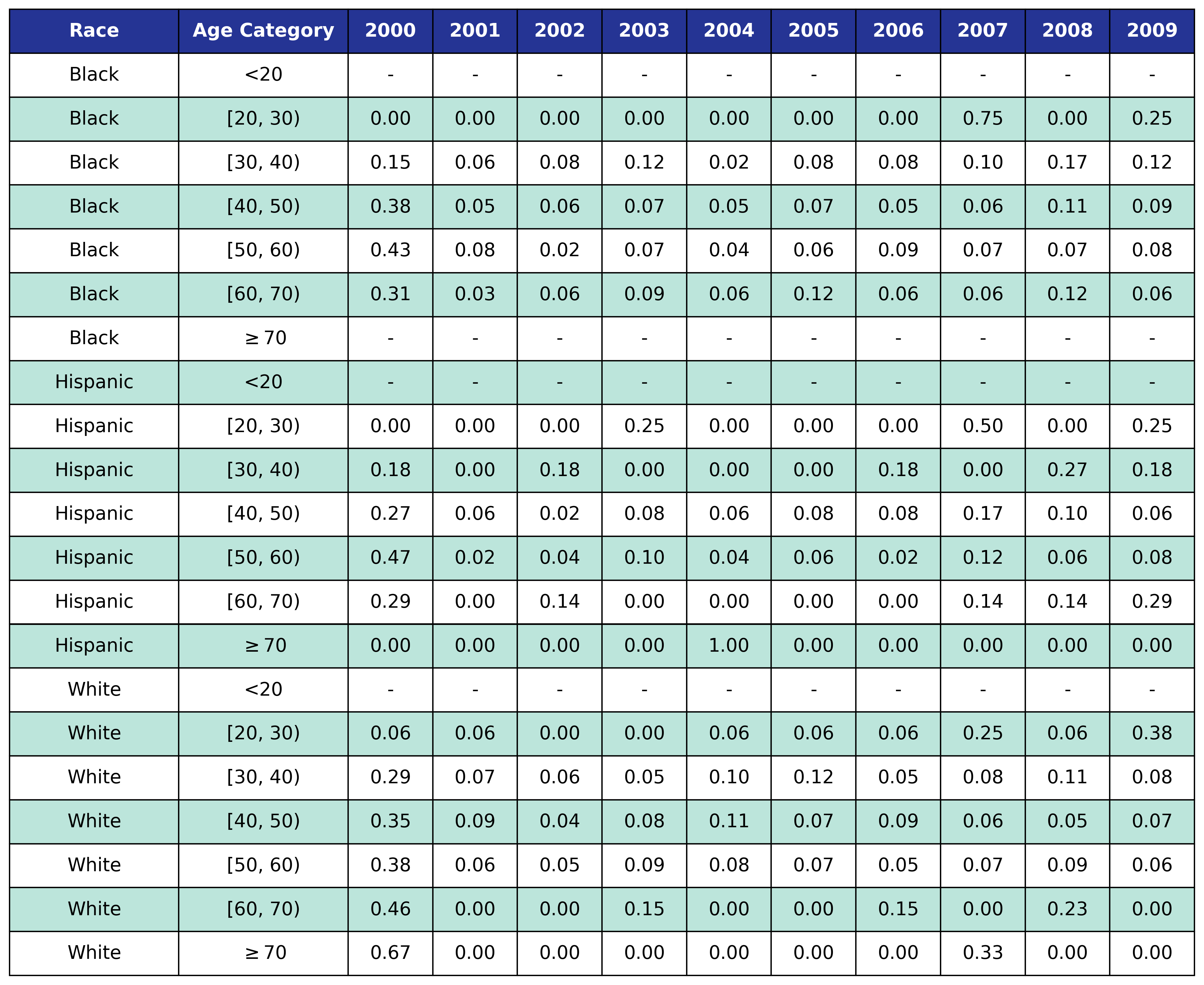
Table 4d: IDU Male
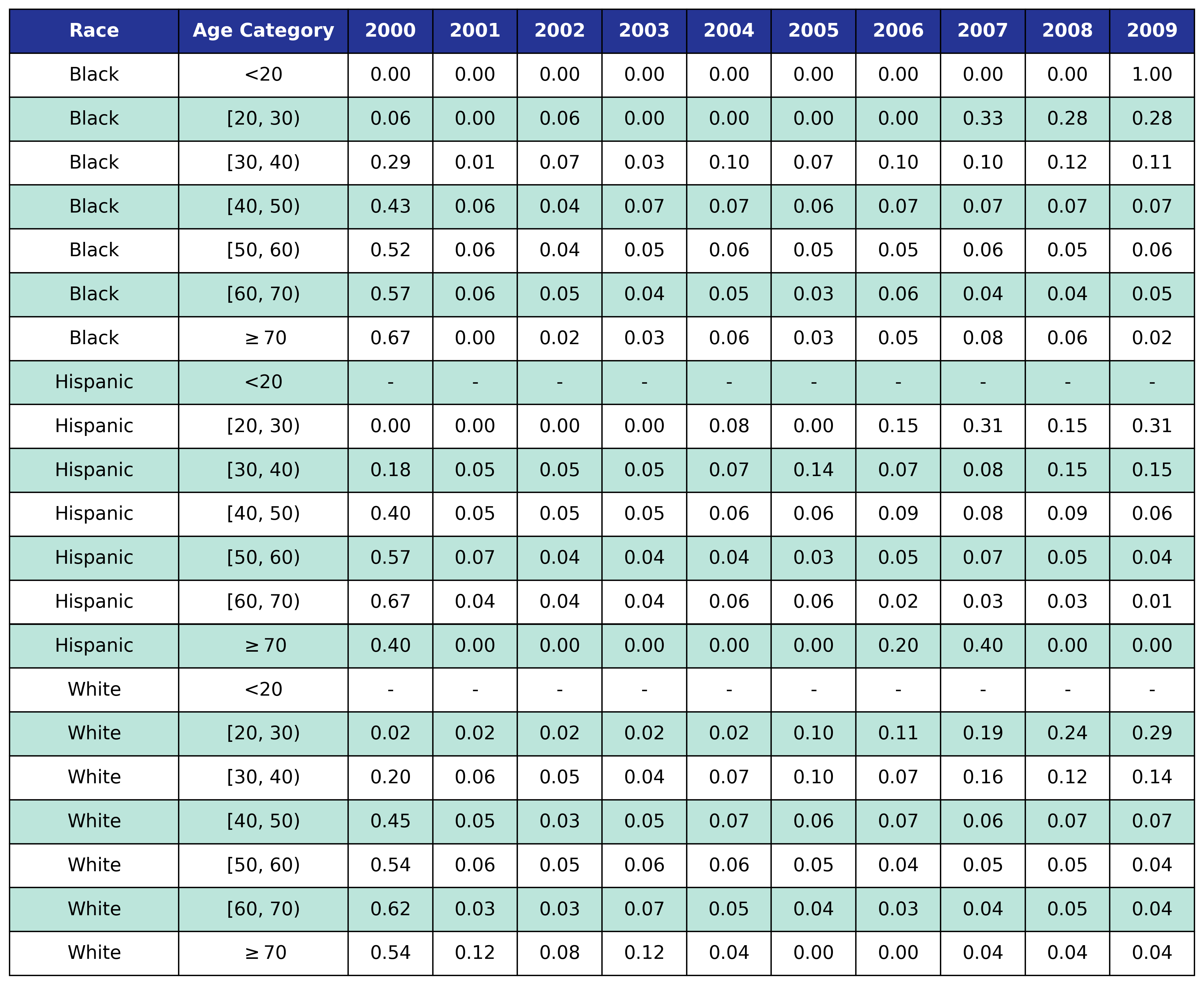
Table 4e: MSM
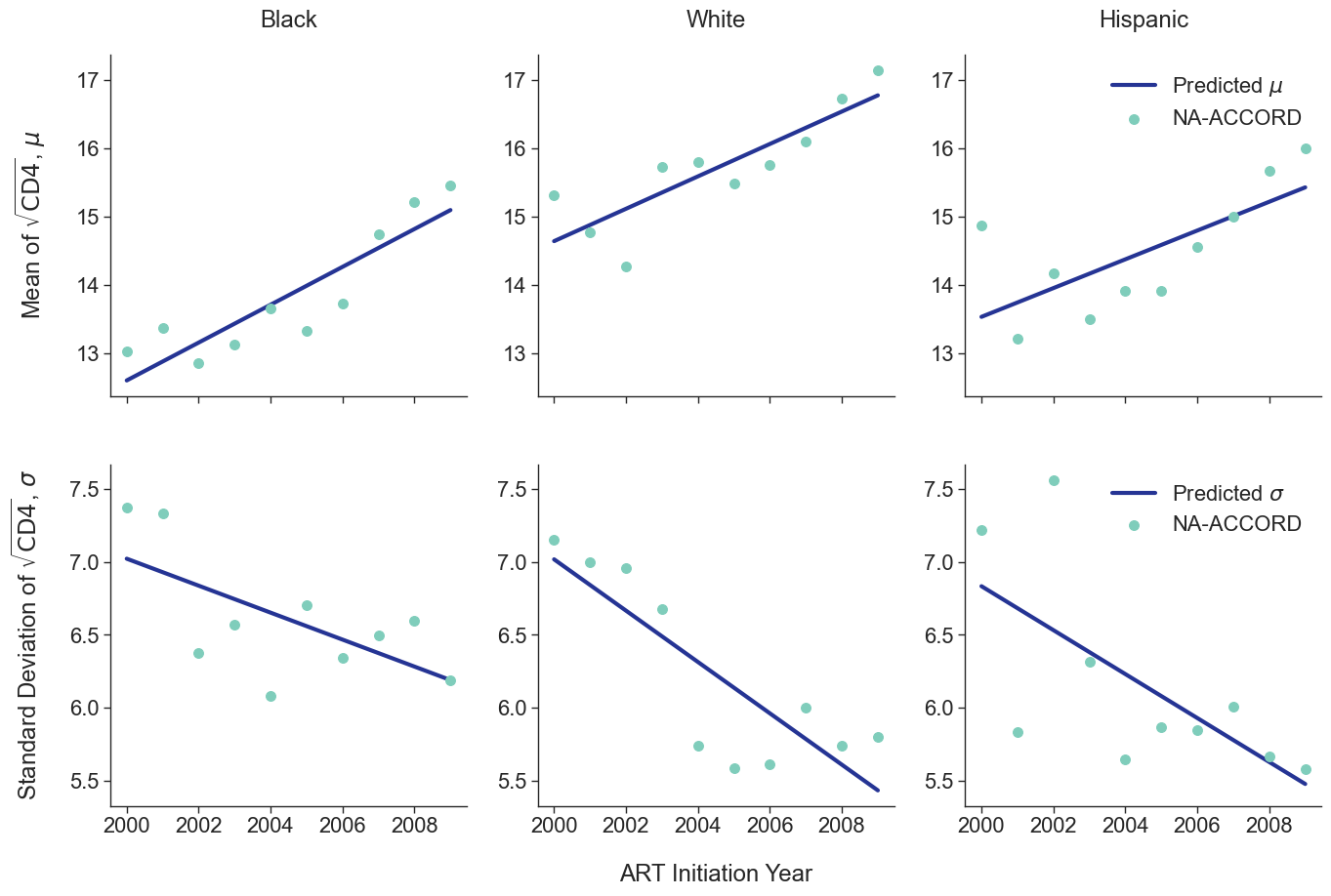
CD4 Count at ART Initiation
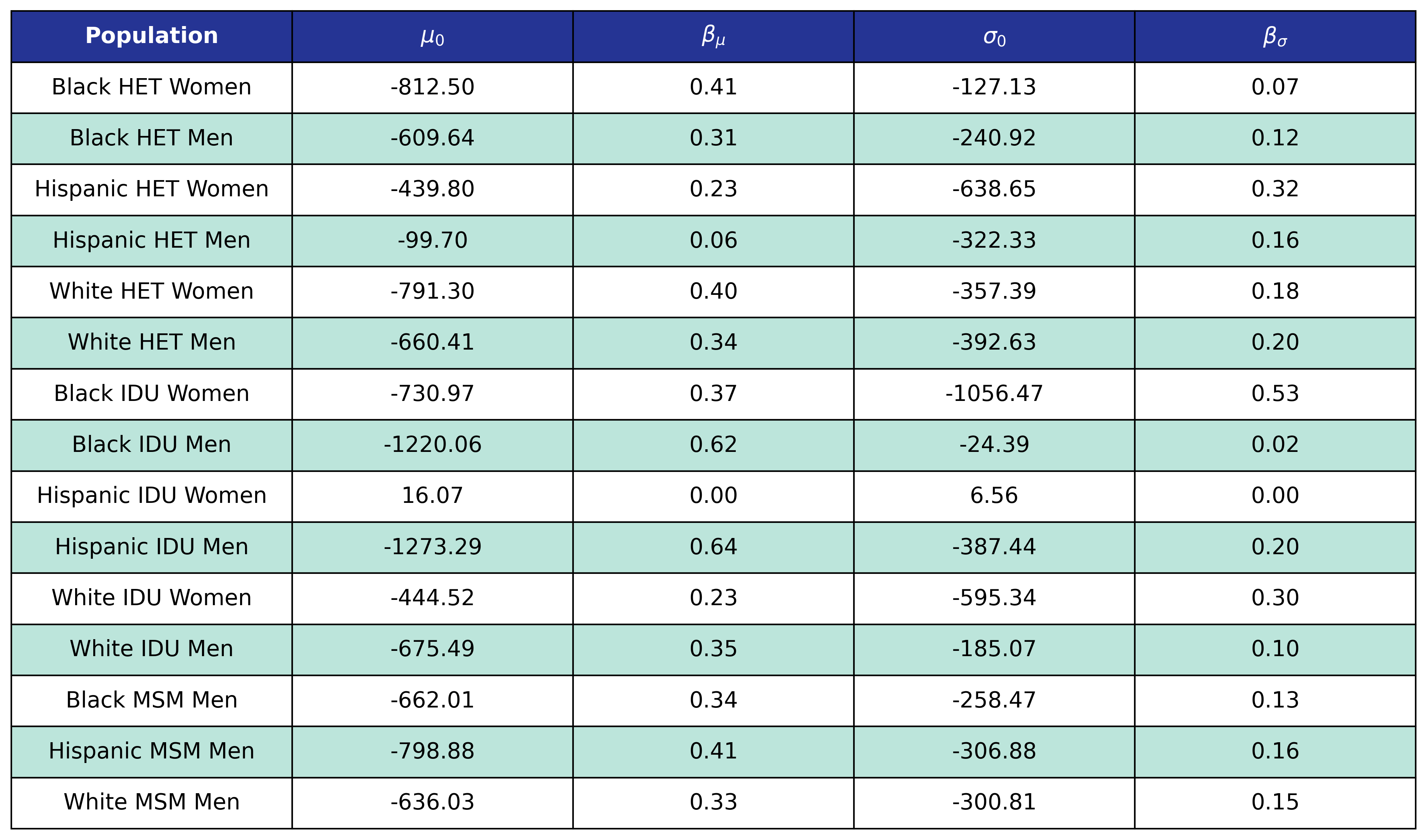
To estimate the CD4 count at first ART initiation among simulated population in year 2009, we applied available data from the NA-ACCORD population on ART in year 2009. To this end, each sub-population was split into original ART initiation years between [2000, 2009] as estimated in the previous step. A normal distribution was fit to describe the \(\sqrt{\mathrm{CD4}}\) count at ART initiation in each year. Within each sub-population, a linear regression model was applied to describe changes in the normal distribution parameters (\(\mu\) mean and \(\sigma\) standard deviation) over time, such that
\[\mu(\mathrm{year}) = \mu_0 + \beta_\mu \cdot \mathrm{year}\]and
\[\sigma(\mathrm{year}) = \sigma_0 + \beta_\sigma \cdot \mathrm{year}\]The linear regression was fit using the glm function of the stats package in base R. Table 5 presents the value of the fitted coefficients.
Table 5: Initial Population CD4 Count at ART Initiation Coefficients
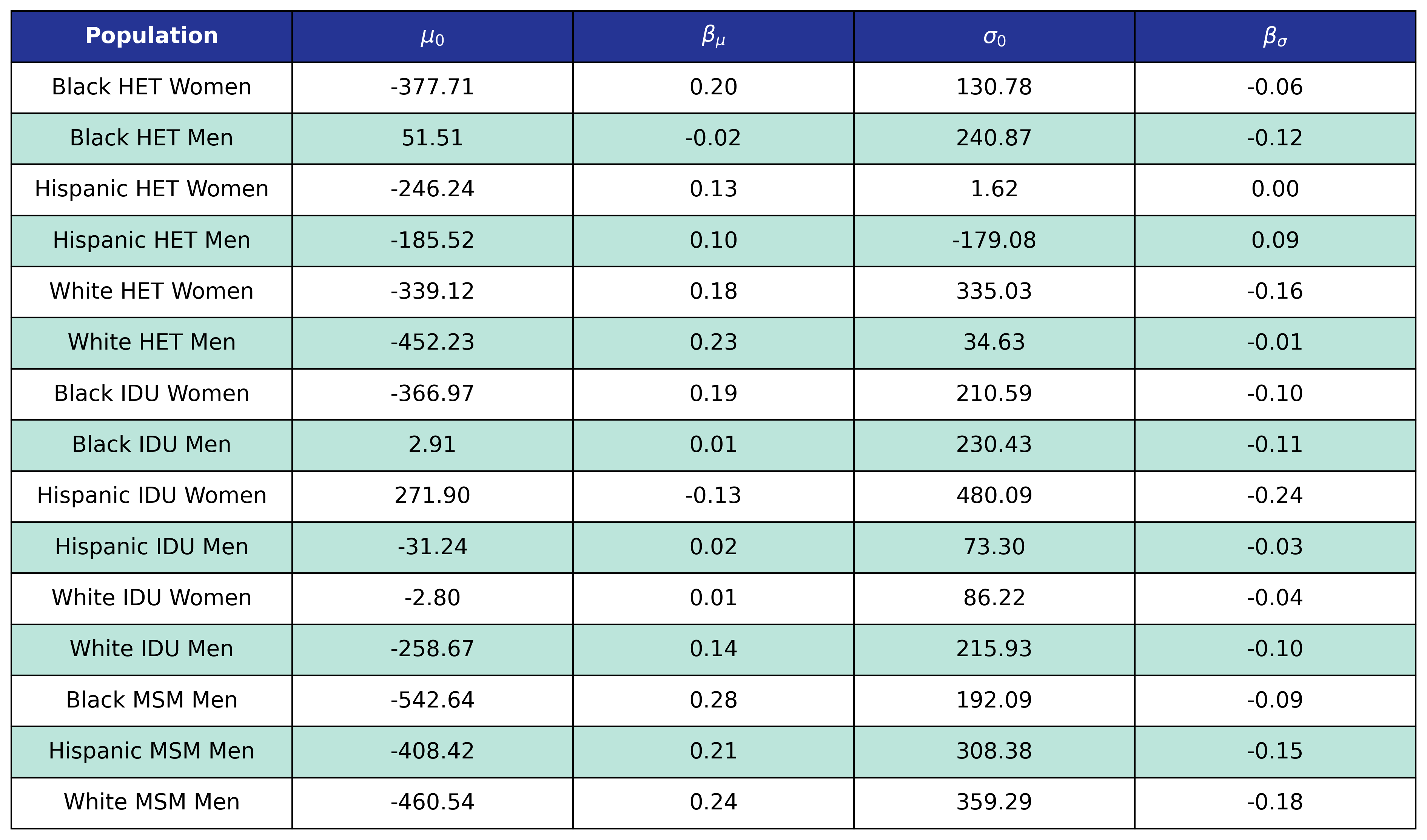
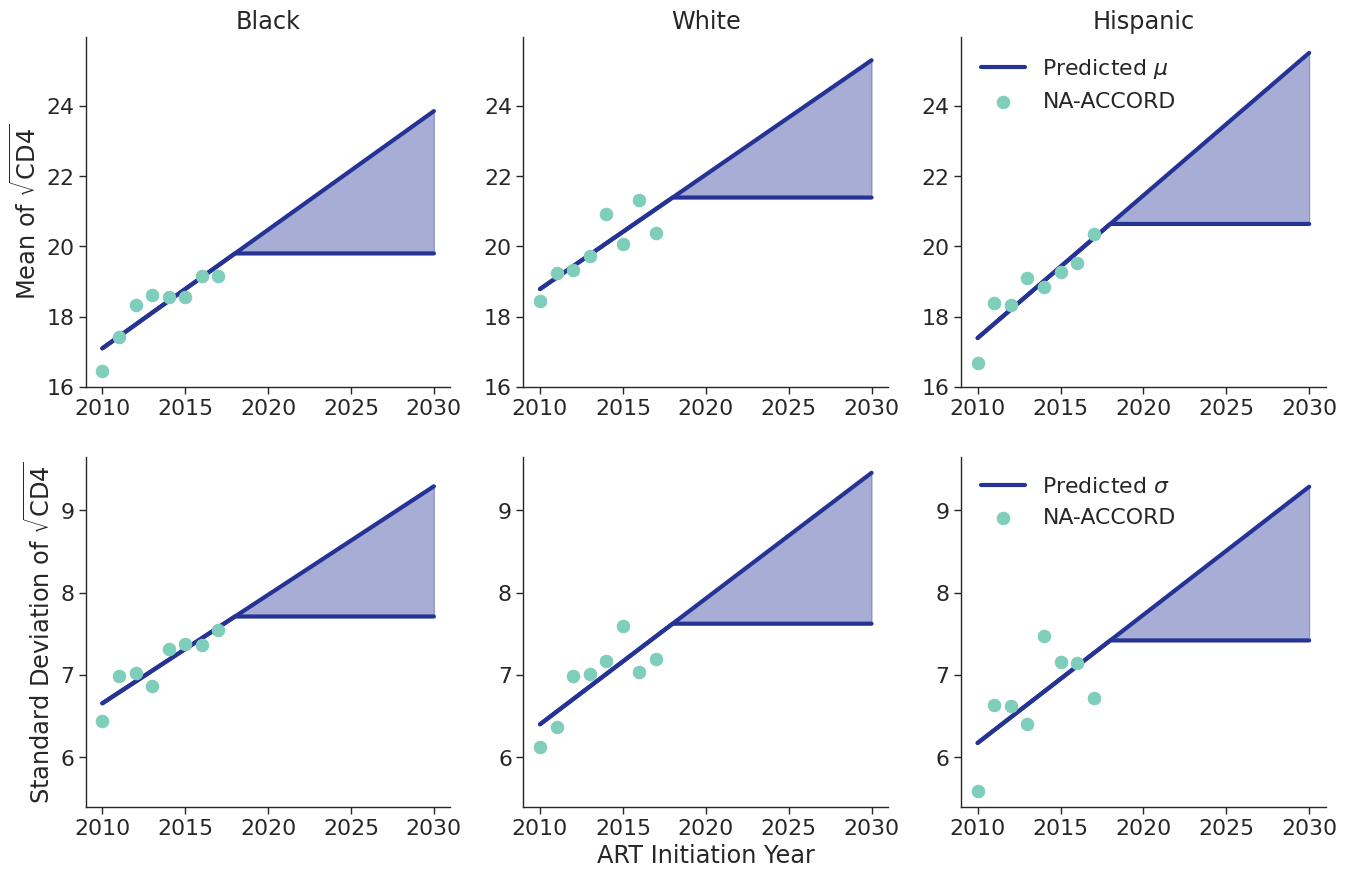
When drawing CD4 values, we truncate the normal distribution at $0$ and $\sqrt{2000}$. The trajectory of the means and standard deviations is shown in the following plots:
Figure 2a: HET Female
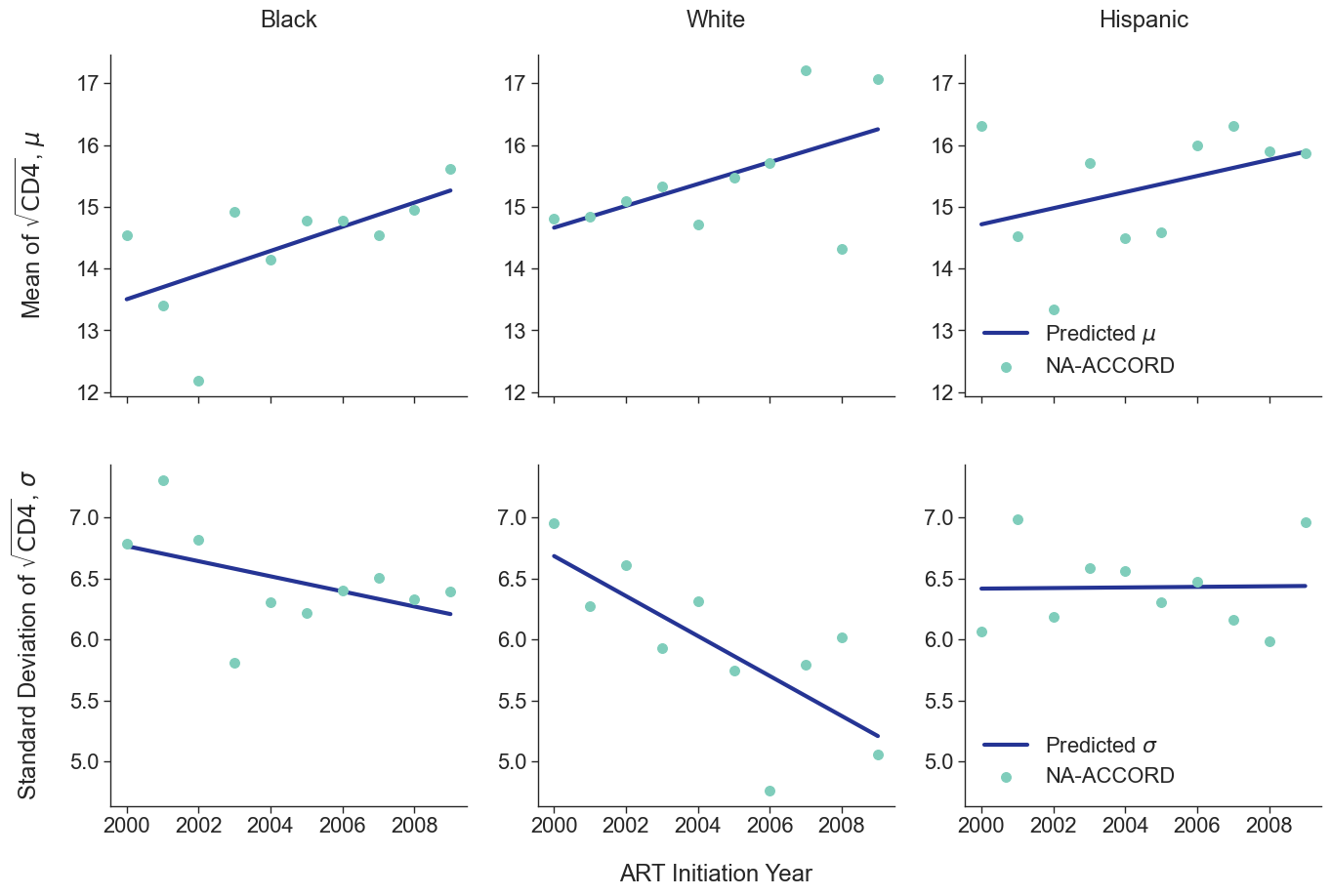
Figure 2b: HET Male
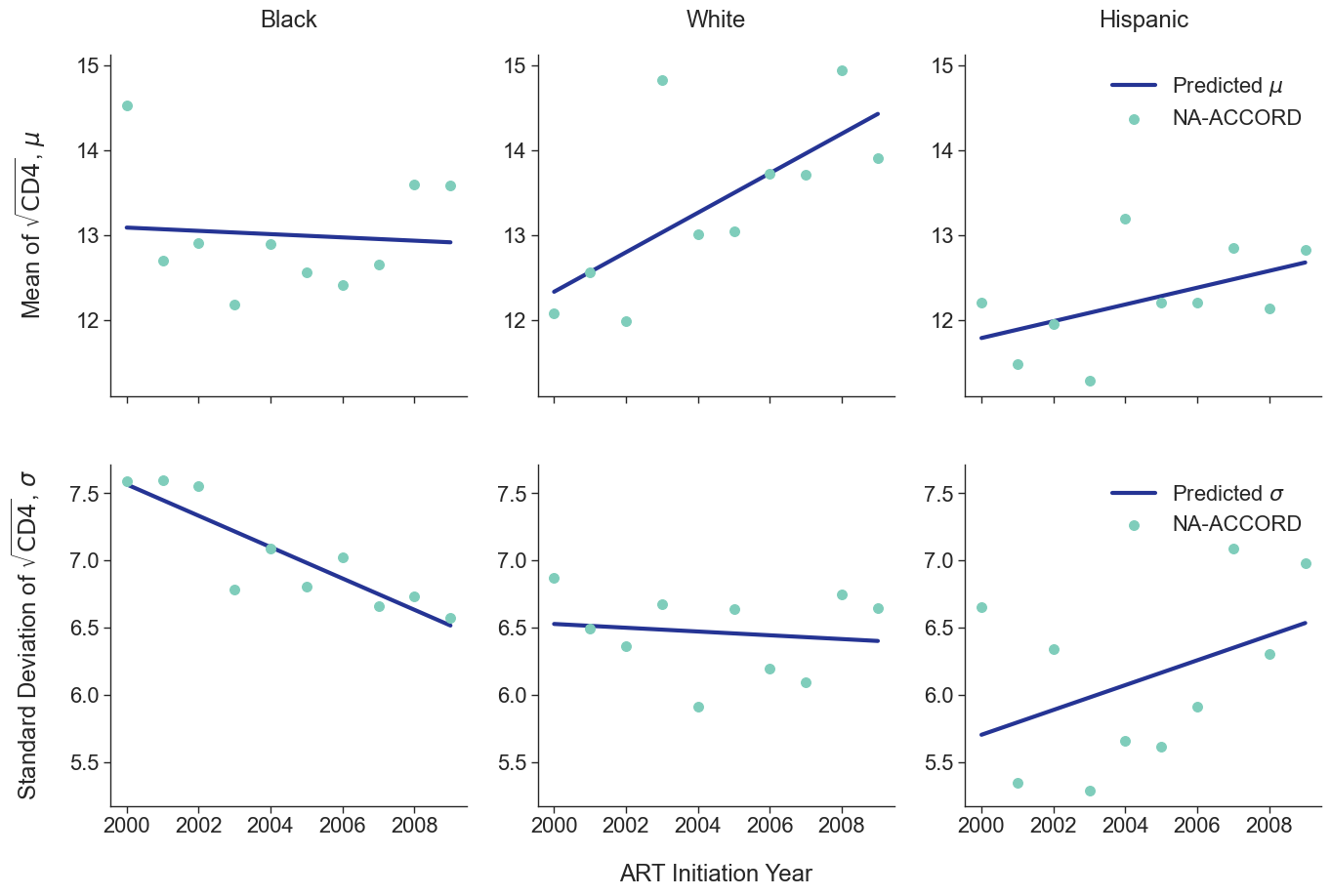
Figure 2c: IDU Female
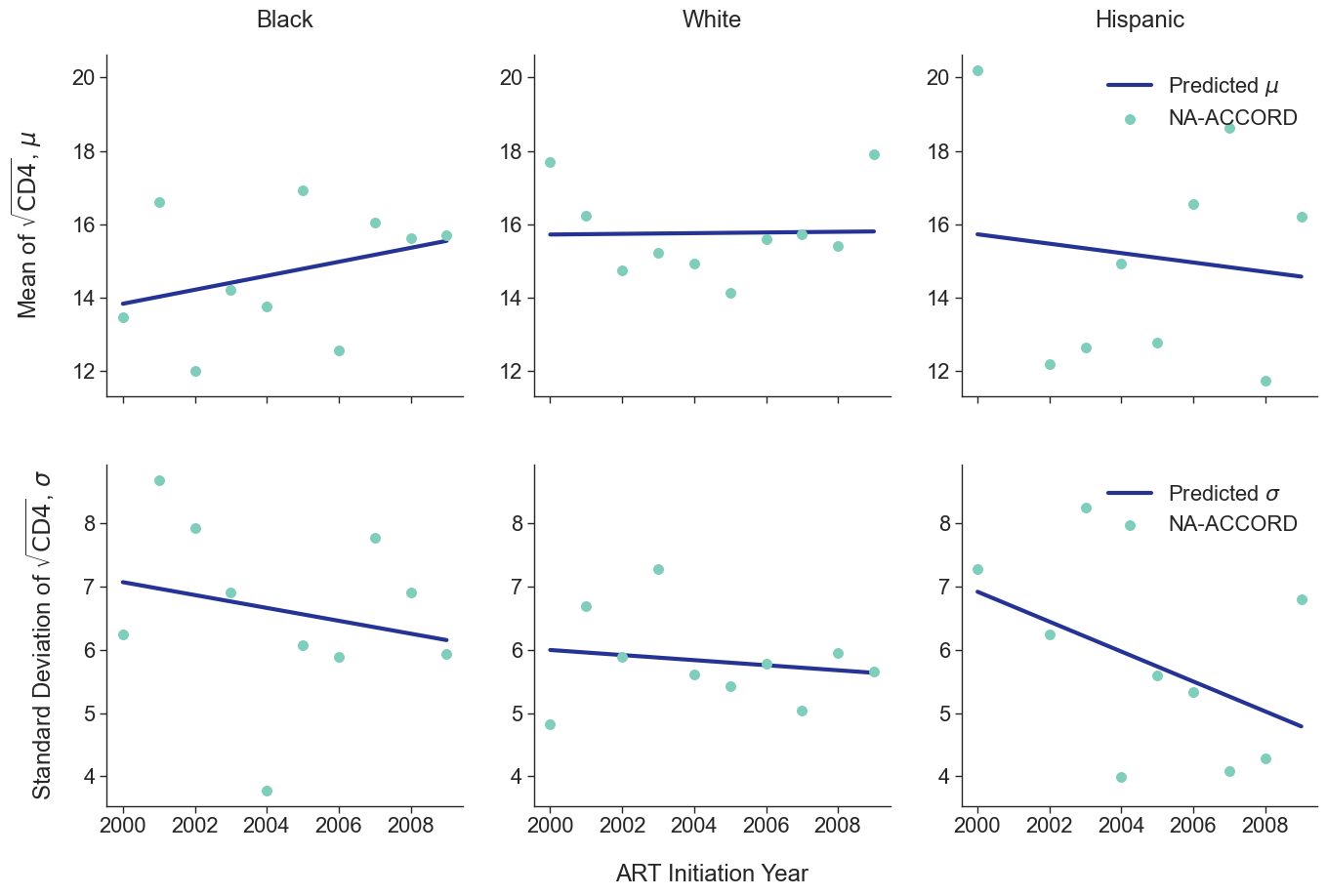
Figure 2d: IDU Male
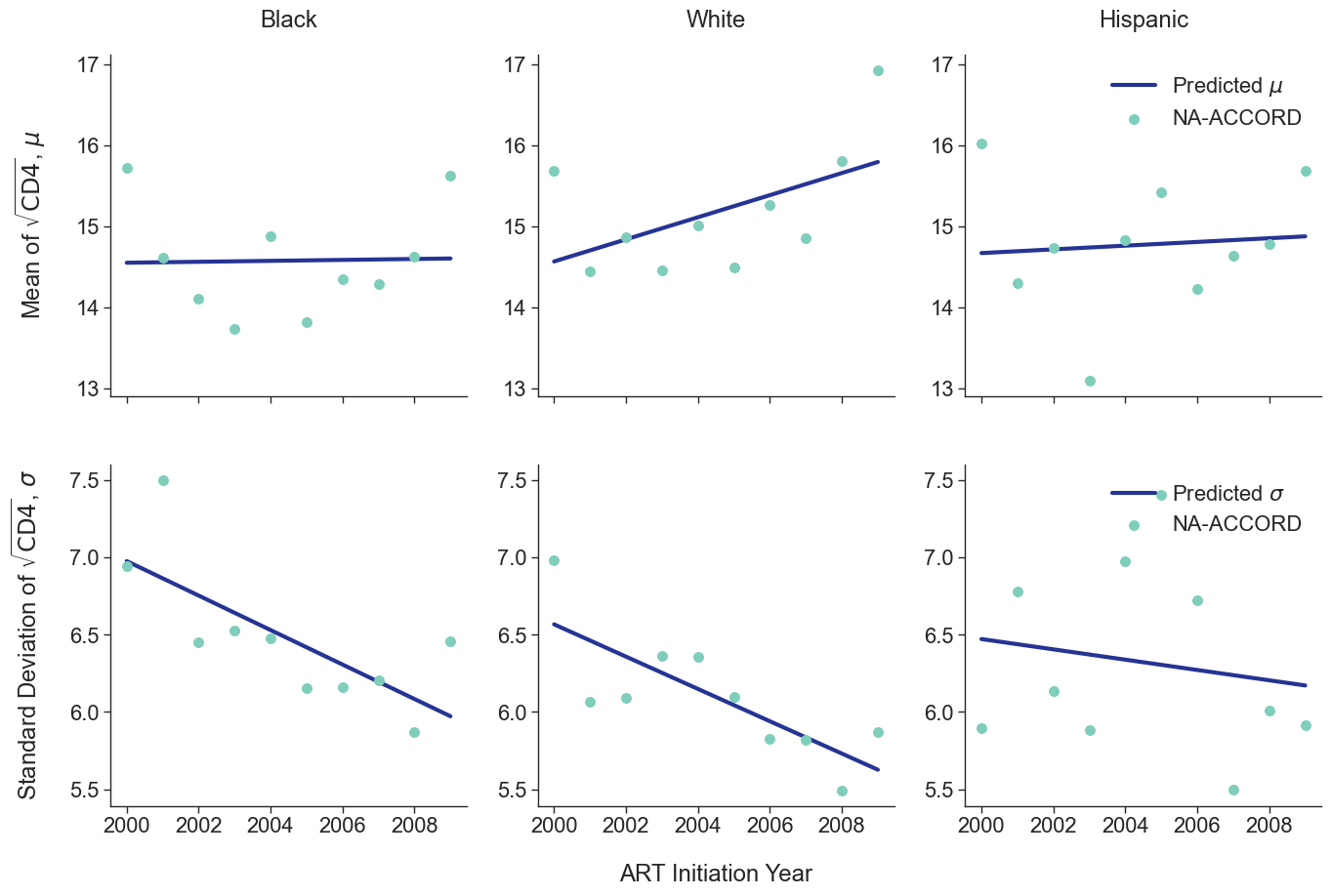
Figure 2e: MSM
Initial Population not Using ART in Year 2009
In addition to an initial population of people on ART in 2009 the simulation is seeded with an initial population of those who had previously been on ART but are currently disengaged from care (and experience a likelihood of ART re-engagement in year 2010 and afterward). The size of this population is generated by estimating the number of those linking to care but not initiating ART from 2006 to 2009 as outlined in the following section. The age and CD4 count distributions for this population is assumed to be identical to the initial ART using population.
Population Initiating ART From 2010 - 2030
Population Size
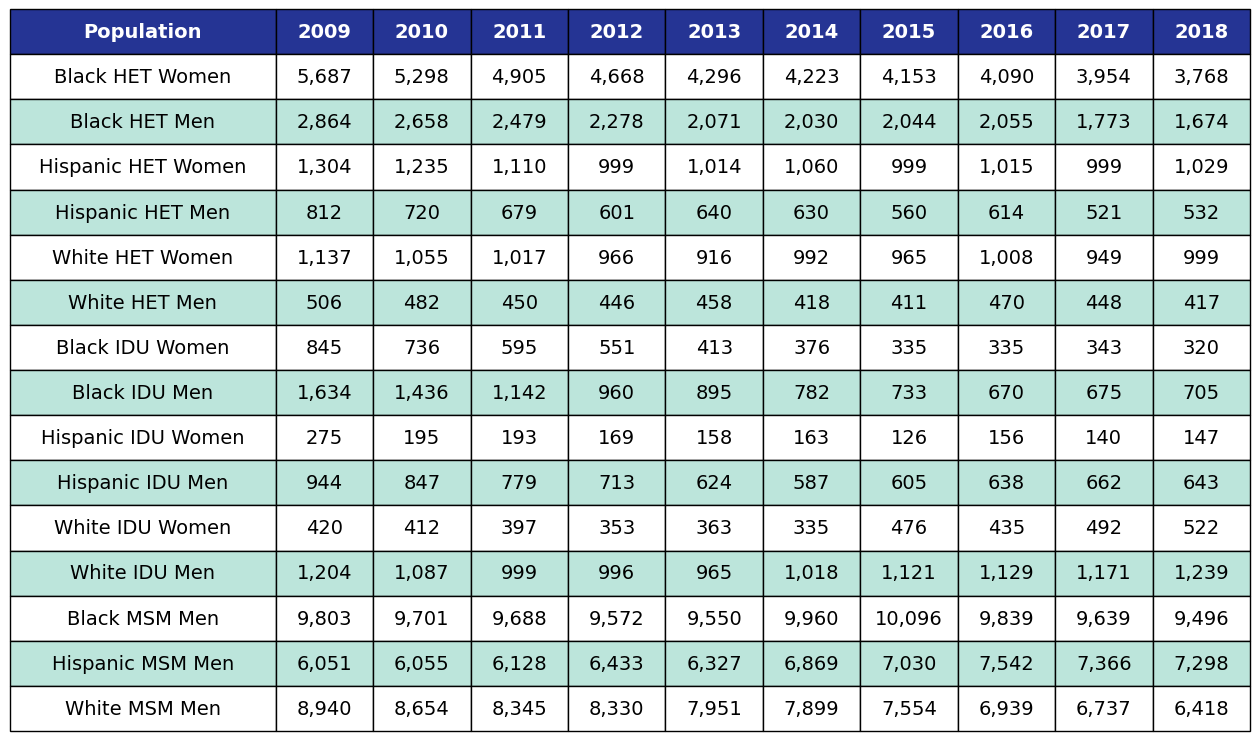
New HIV diagnosis: In order to predict the number of new people linking to HIV care and starting ART in a given year, we begin with data on the number of new HIV diagnoses per year as estimated by the CDC’s Medical Monitoring Project (MMP) as shown in Table 6. Dates before 2016 came from Table 1 of the 2015 HIV Surveillance Report, while data 2016 and after came from Table 1 of the 2018 HIV Surveillance Report.
Table 6: Number of New HIV Diagnoses by Year
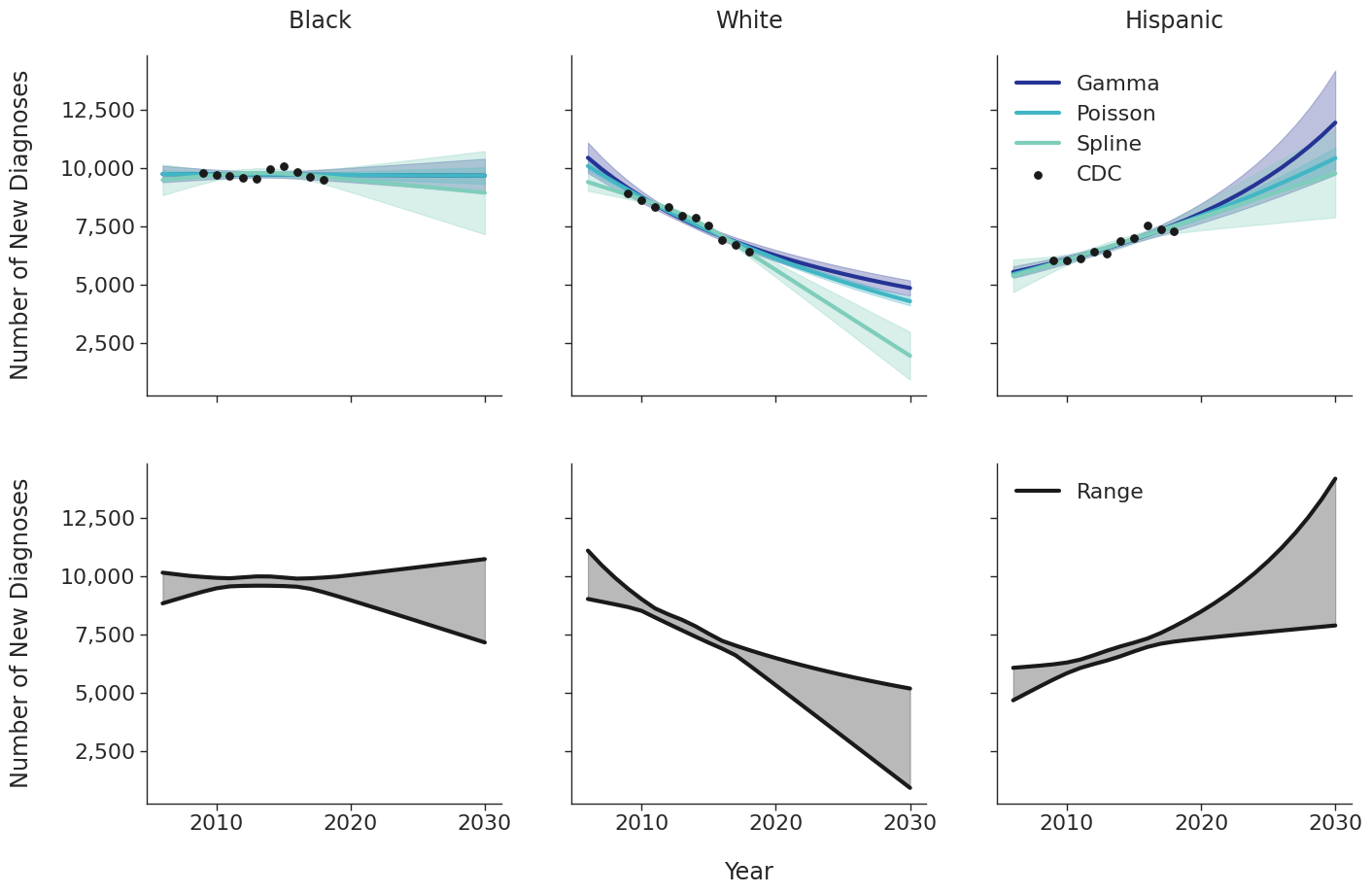
Various candidate models were proposed in order to predict the number of new HIV diagnoses from 2006 to 2030. Predicted HIV diagnoses prior to 2010 are used later in the initial 2009 population creation. After removing models with inadequate fit (based on AIC values), the data were fit using a Poisson model, a gamma model and a natural cubic spline model with a single knot. Of these models, those resulting in unrealistic projections (>50% increase in new diagnosis from 2020 – 2030) were also removed. The Poisson and gamma fits were accomplished using the glm function of the stats package in base R, while the spline fit was generated using the lm and ns functions of the base R packages stats and splines, respectively. To incorporate additional uncertainties in annual estimates, the 95% prediction intervals around each fit were calculated. These prediction intervals were combined to generate an annual range for the number of new diagnosis in each year for a given subgroup (black, white and Hispanic). The annual ranges are estimated from the largest upper prediction interval and the lowest lower prediction interval of existing models as shown in panel 2 of Figure 3. For each simulation run, a random number between 0 and 1 is drawn that defines the number of new diagnoses in that simulation. Figure 3 shows the full ranges used to generate the number of new diagnoses.
Figure 3a: HET Female
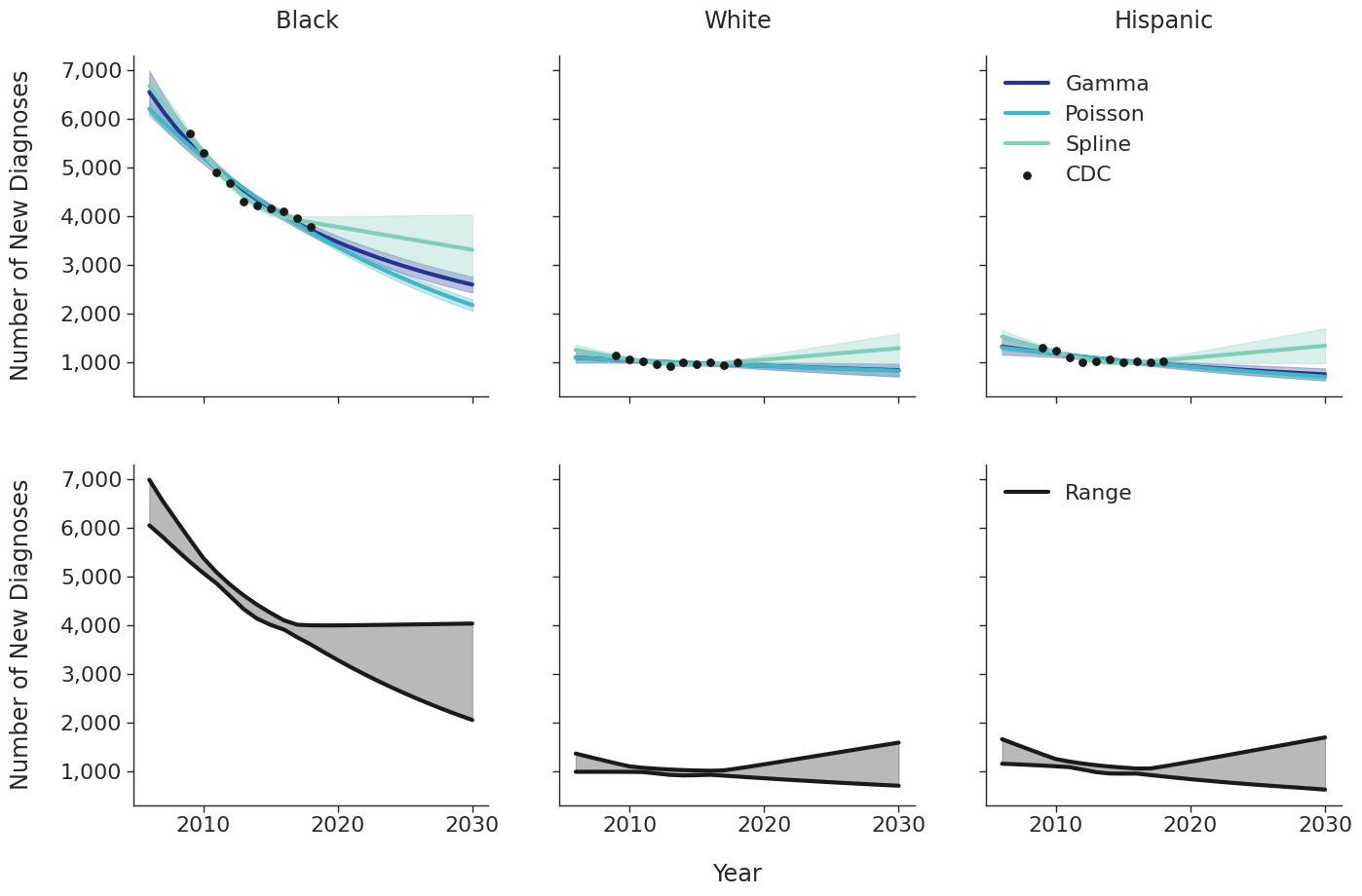
Figure 3b: HET Male
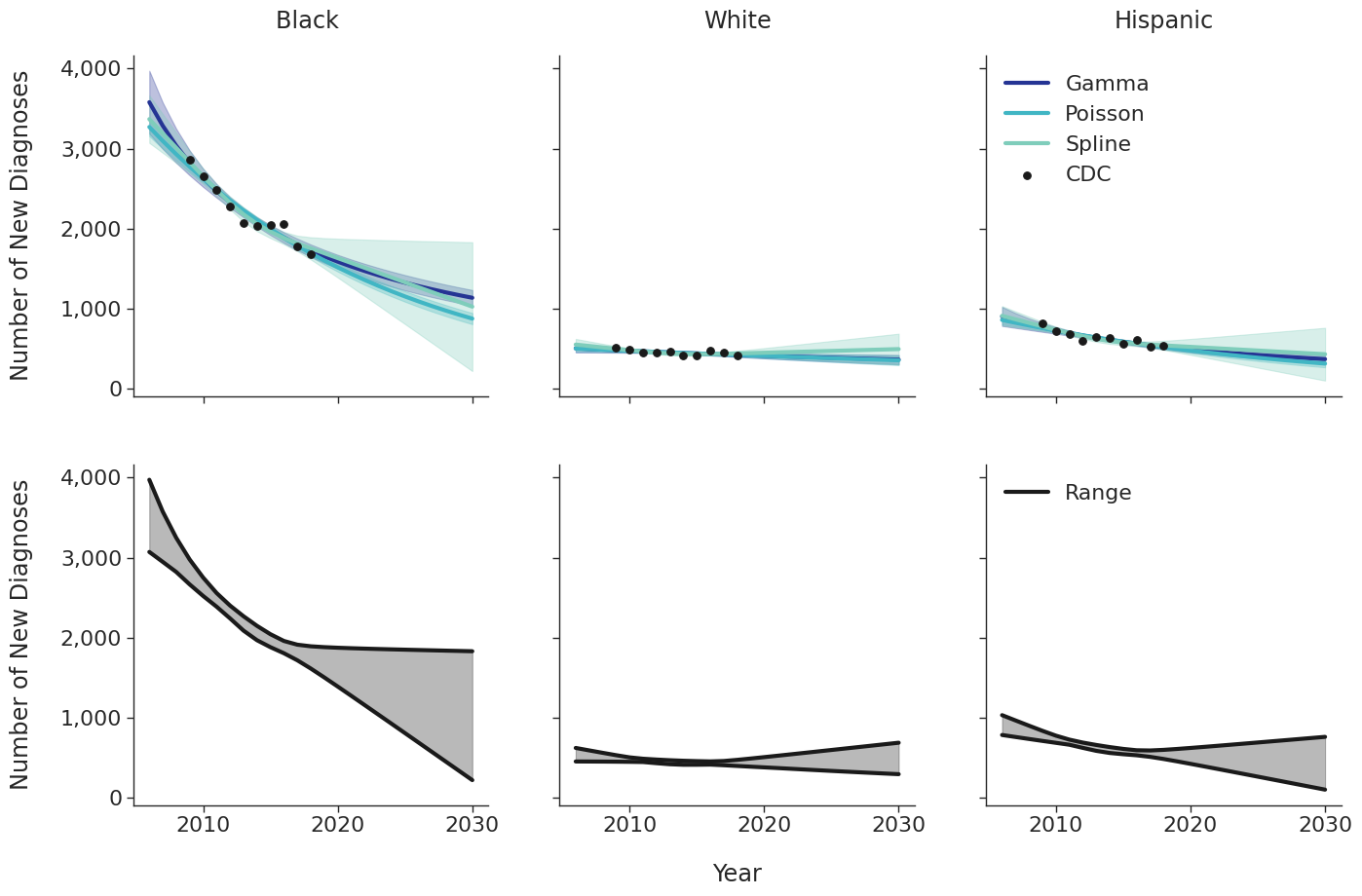
Figure 3c: IDU Female
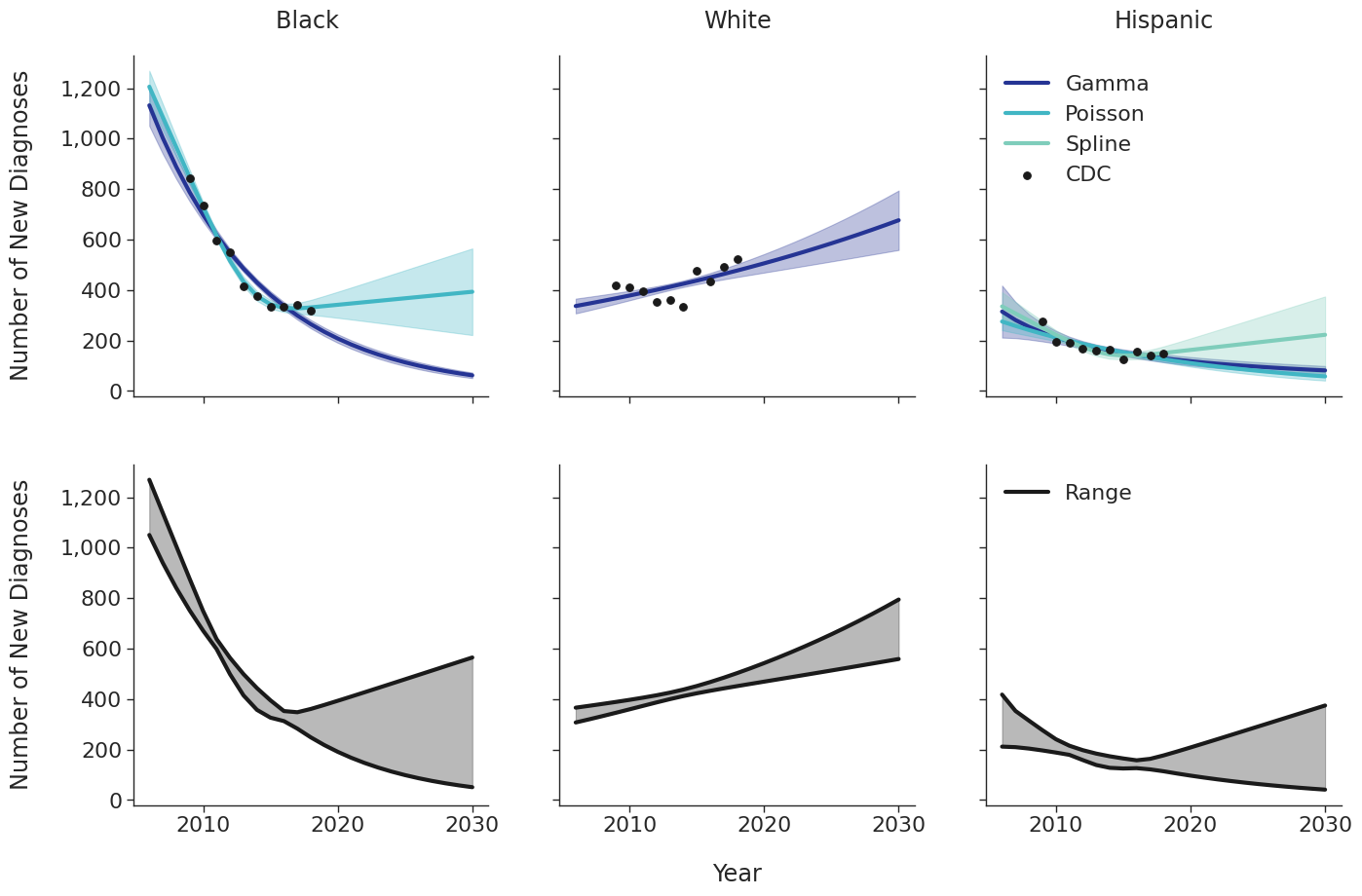
Figure 3d: IDU Male
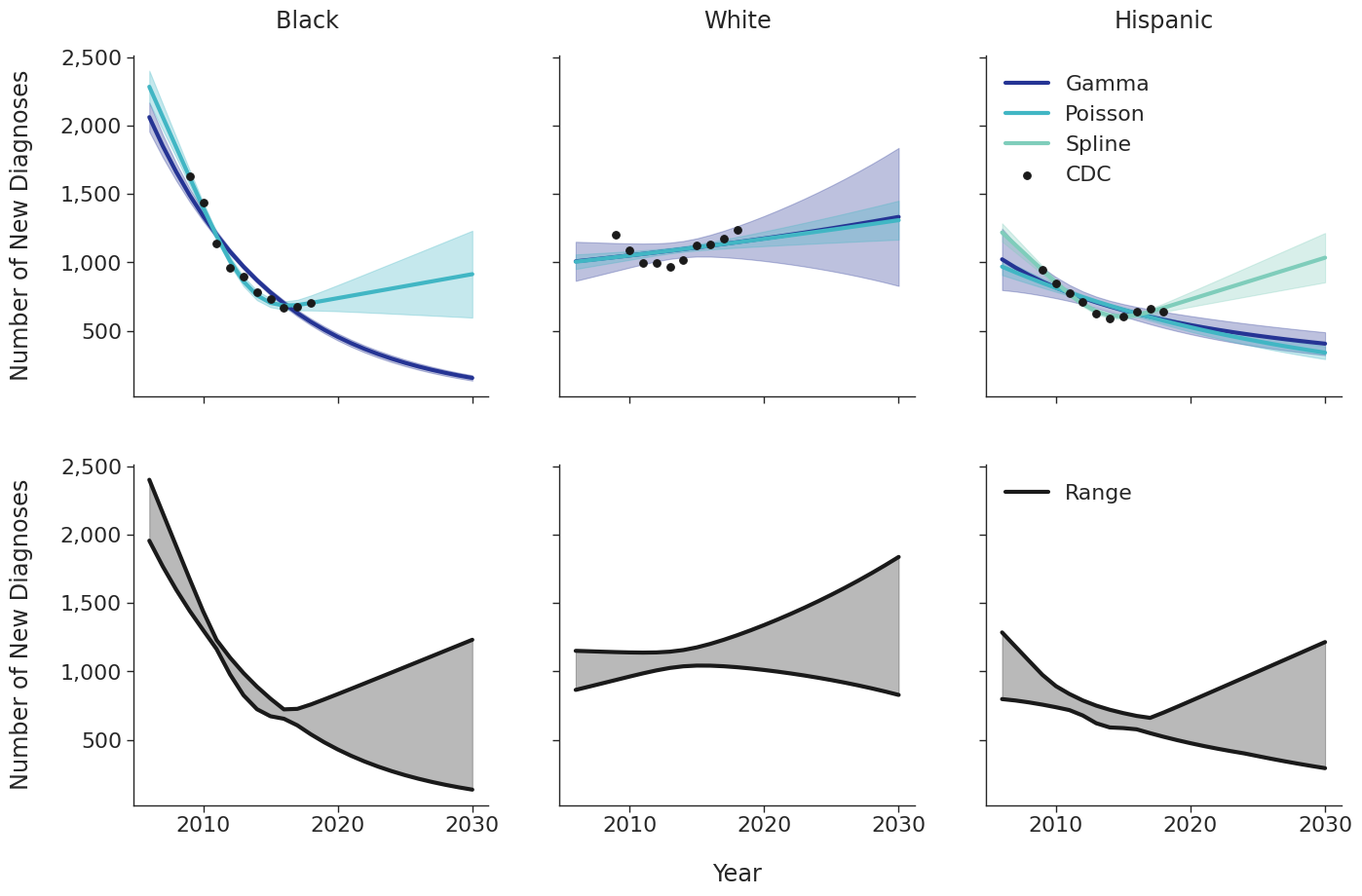
Figure 3e: MSM
Linkage to HIV care and ART initiation: We estimated percentage of people in each sub-population linking to HIV care in the first 4 months after HIV diagnosis for each year between 2010 – 2015 from the CDC. To project future trends from 2016 to 2030, we applied a linear regression and capped at 95% linkage as shown in Figure 4. The linear regression was accomplished using the ols function of the statsmodels package for Python. Among remaining cases, we further assumed that 40% link to care over the next three years after initial diagnosis. To estimate the population starting ART, we assumed that 70% of those linking to care begin ART immediately in years prior to 2011. This percentage rises to 85% in 2011 and up to 97% thereafter.
Figure 4a: HET Female
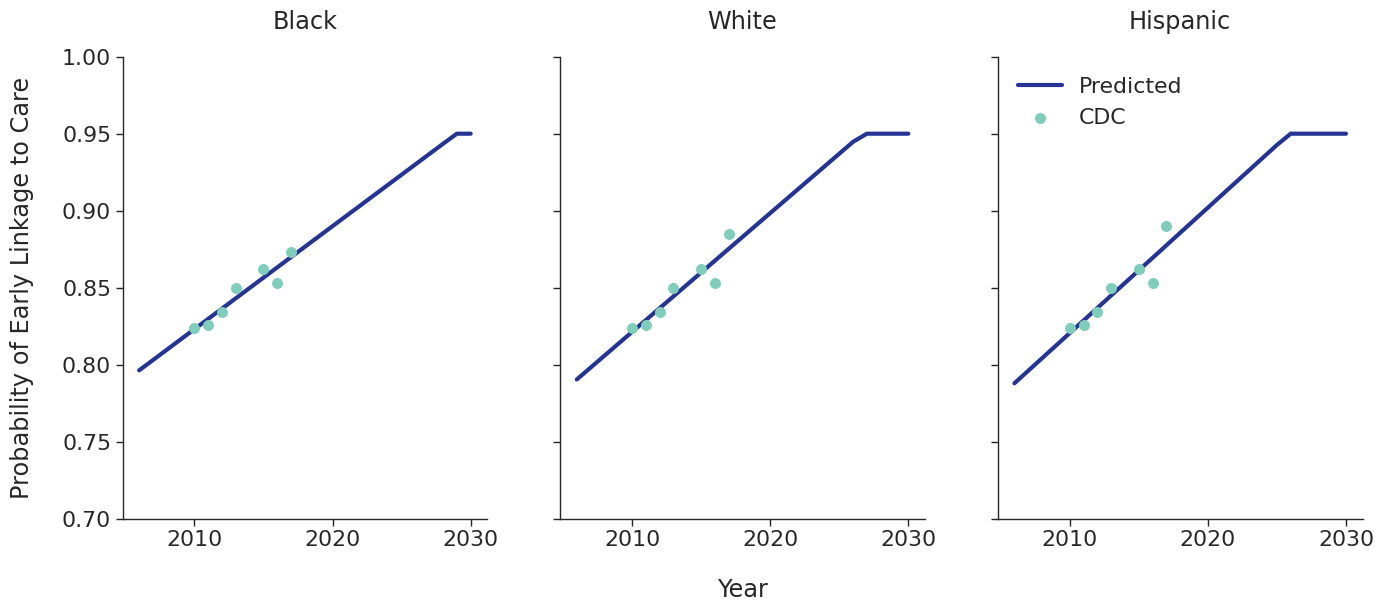
Figure 4b: HET Male
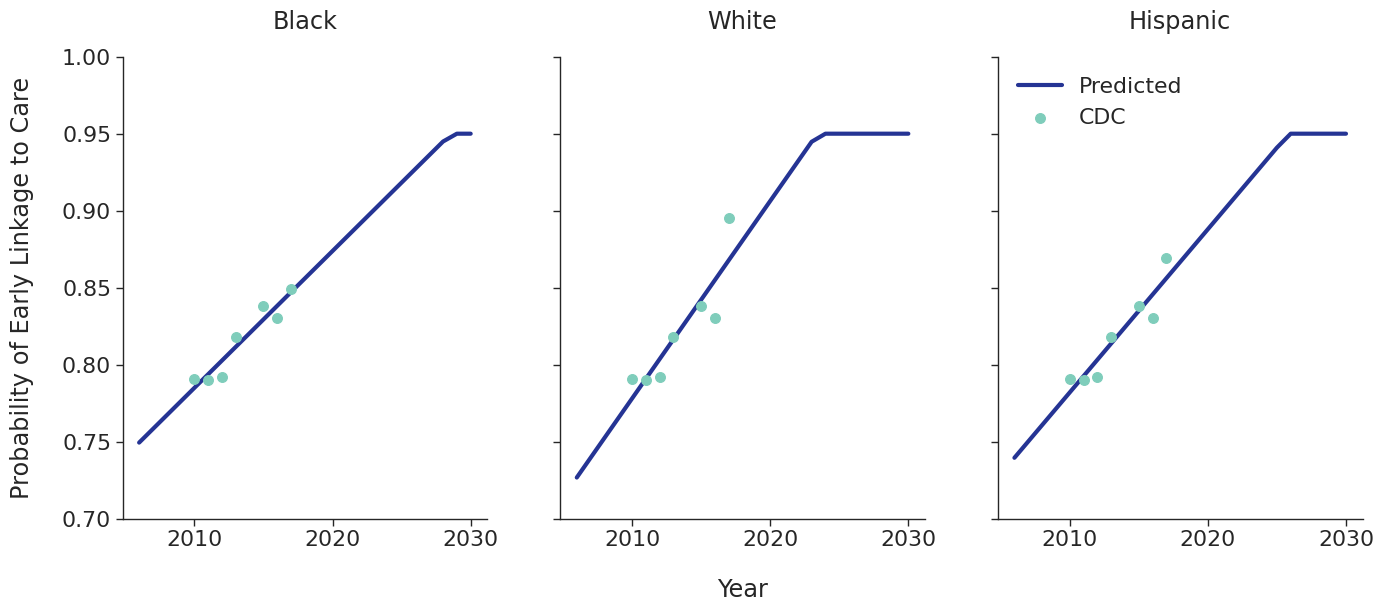
Figure 4c: IDU Female
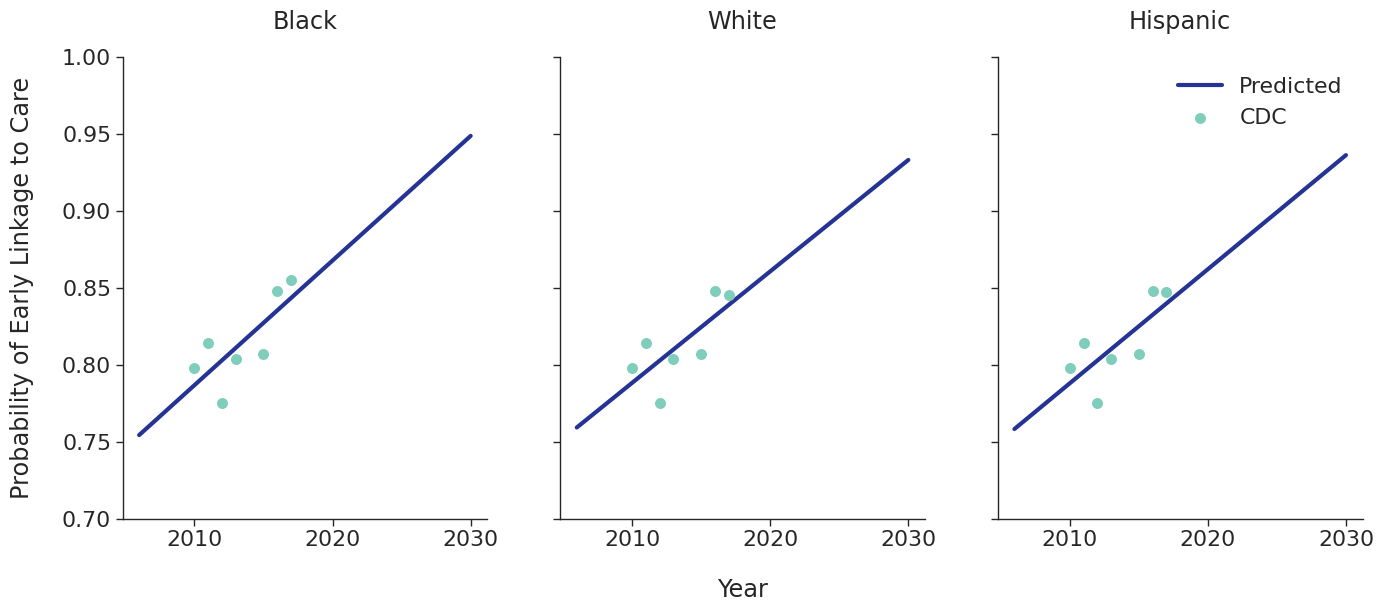
Figure 4d: IDU Male
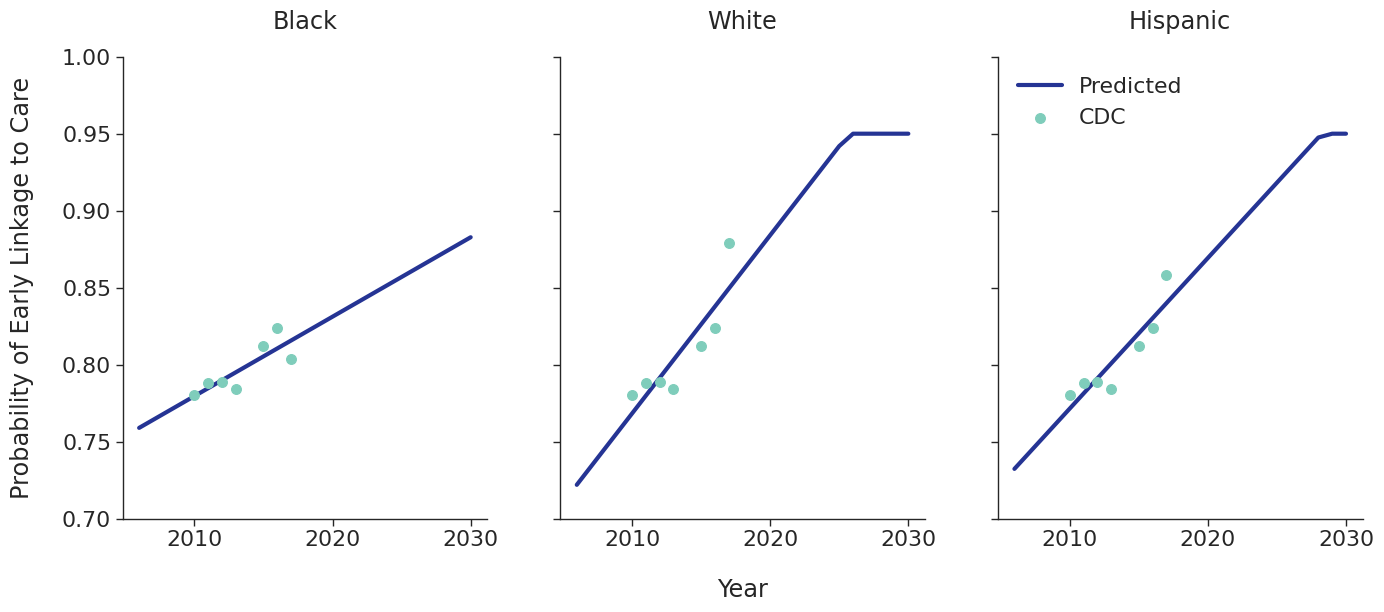
Figure 4e: MSM
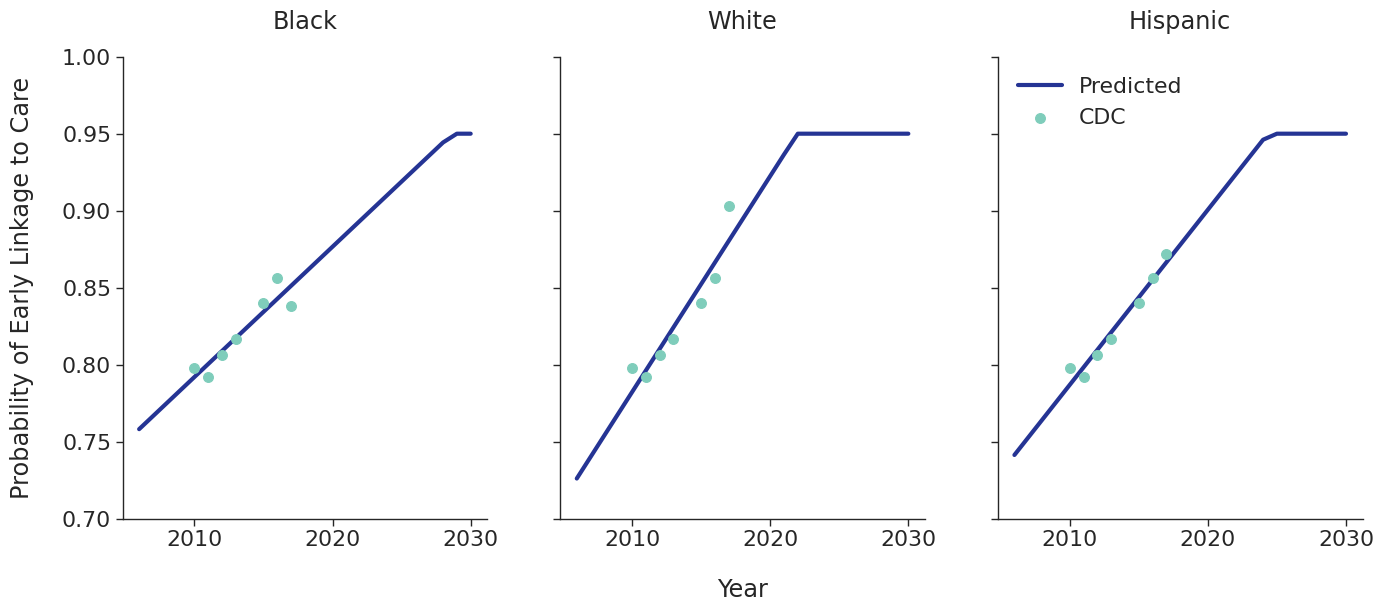
Age Distribution
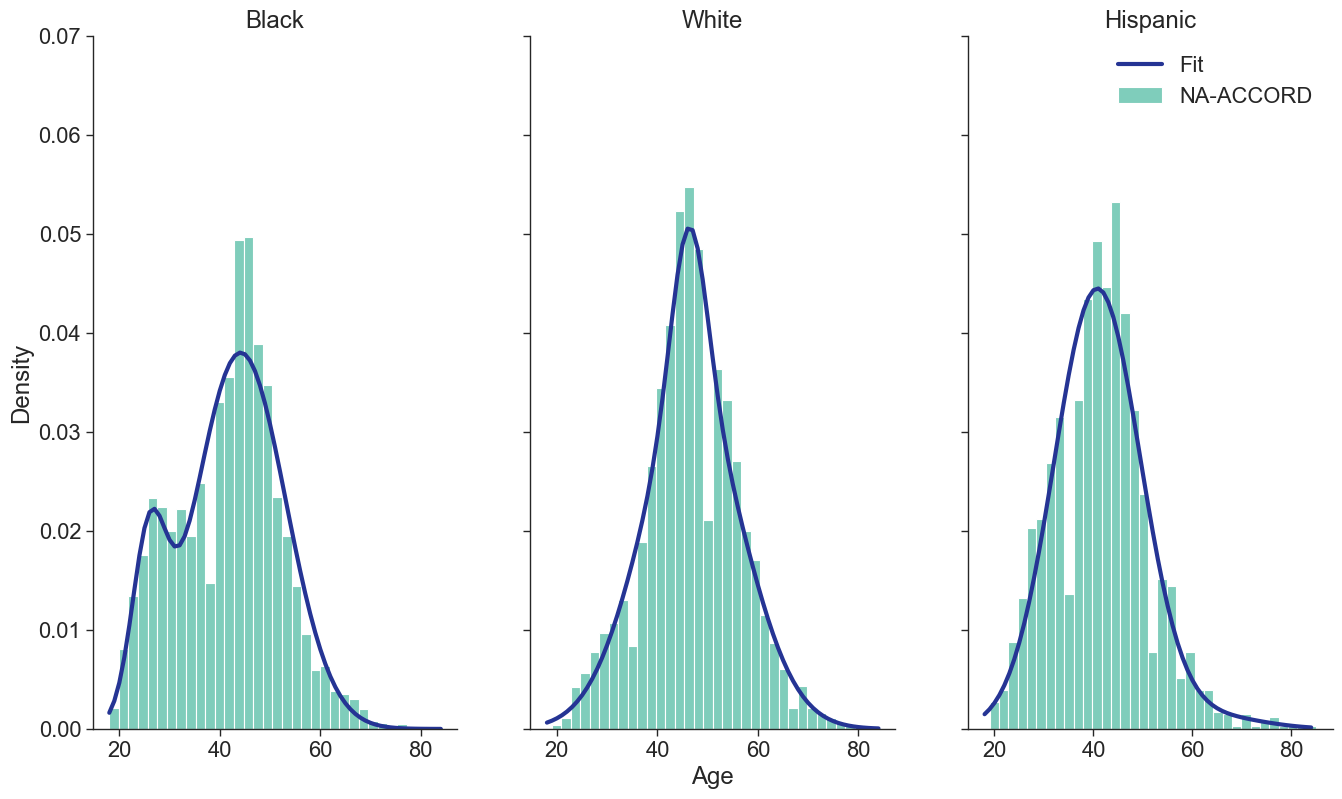
The age distributions of the populations initiating ART in each year are modeled as a two component mixed normal distribution:
\[f(x|\lambda_1, \mu_1, \sigma_1, \mu_2, \sigma_2) = \lambda_1 g(x|\mu_1, \sigma_1) + (1 - \lambda_1)g(x|\mu_2, \sigma_2)\]where
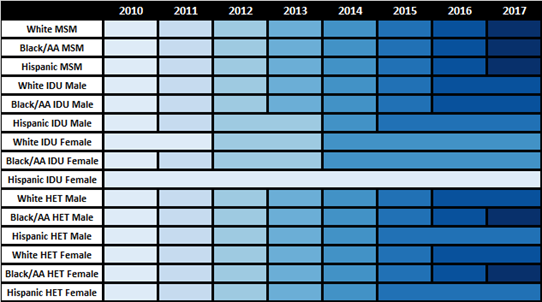
\[g(x|\mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]is the usual normal distribution. Here $x$ represents age at ART initiation, $\lambda_1$ is the mixing proportion, and the $\mu$’s and $\sigma$’s are the means and standard deviations of the bimodal distribution. A fit was found for each ART initiation year, from 2010 to 2017, and each sub-population using data from NA-ACCORD using the normalmixEM function of the mixtools package for R. Due to lack of available data, some years had to be collapsed together as shown in Figure 5.
Figure 5: Age Distribution Data Collapse
To estimate changes in age distribution of ART initiators over time, we modeled changes in the five parameters of the distribution as a linear function of calendar year (Figure 6). For this purpose, each parameter was fit to a linear regression using the glm function of the stats package in base R (blue dots in Figure 6). Given the sharp rate of change through the linear fit and lack of available data to support predictions from 2018 onward, the predicted values in year 2018 were used as an upper/lower bound to develop a prediction range for future years (shaded areas in Figure 6). Values for \(\lambda\_1\) were truncated between 0 and 1 and all variables are truncated at 0. These models were applied to generate the value of 5 parameters describing the bimodal normal distribution of age at ART initiation in each year. The distribution was further truncated at ages 18 and 85.
Figure 6a: HET Female
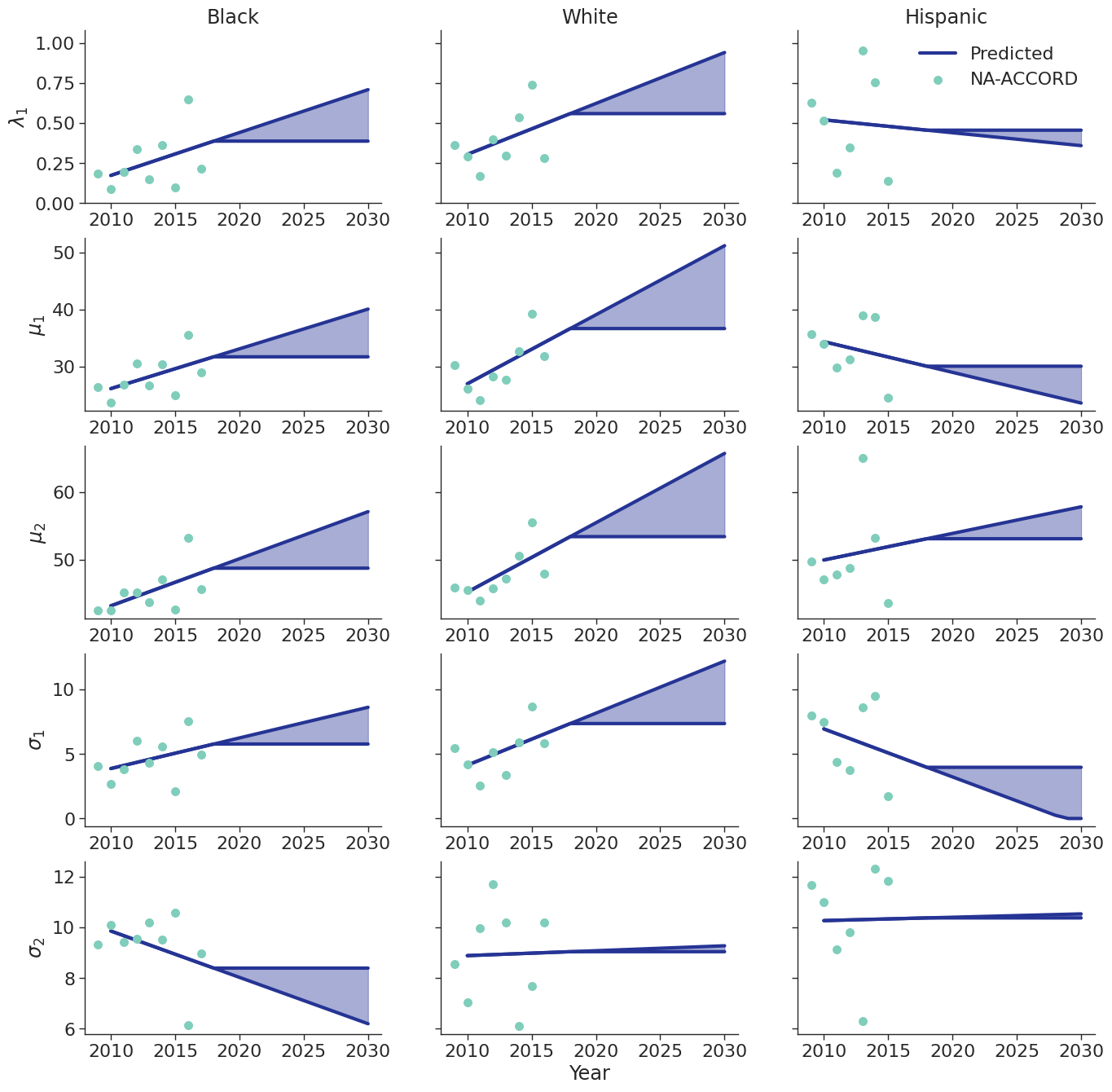
Figure 6b: HET Male
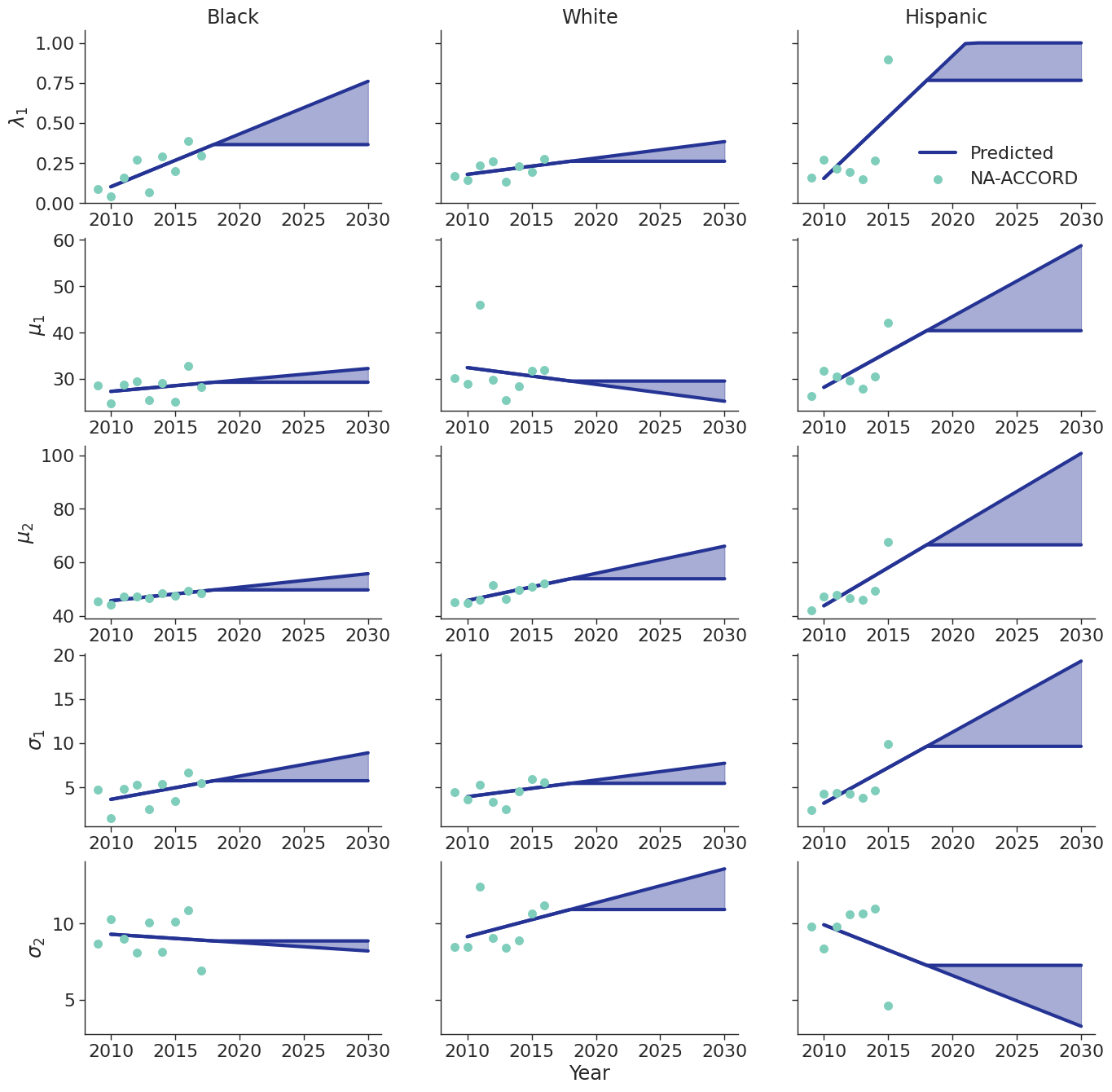
Figure 6c: IDU Female
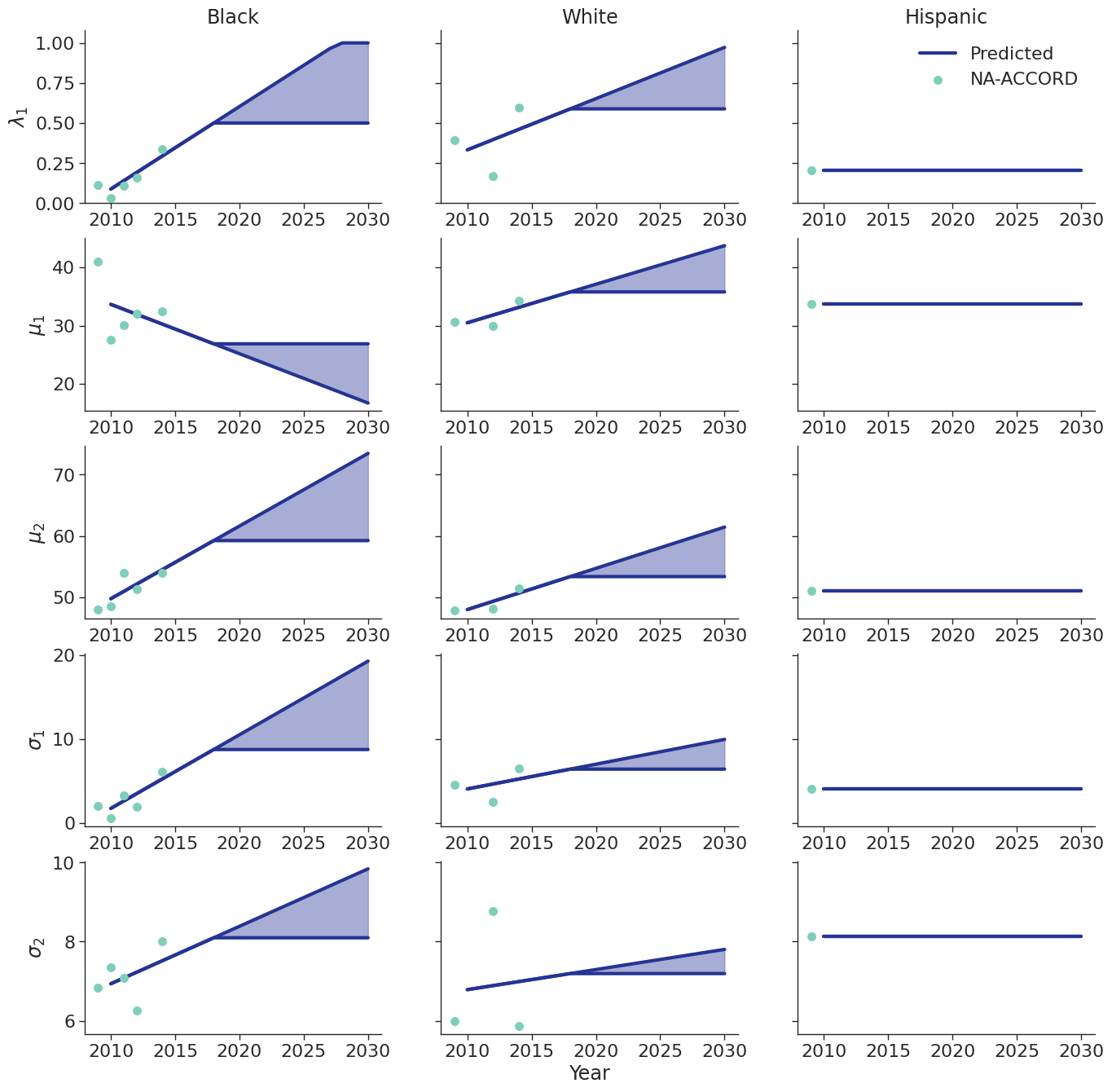
Figure 6d: IDU Male
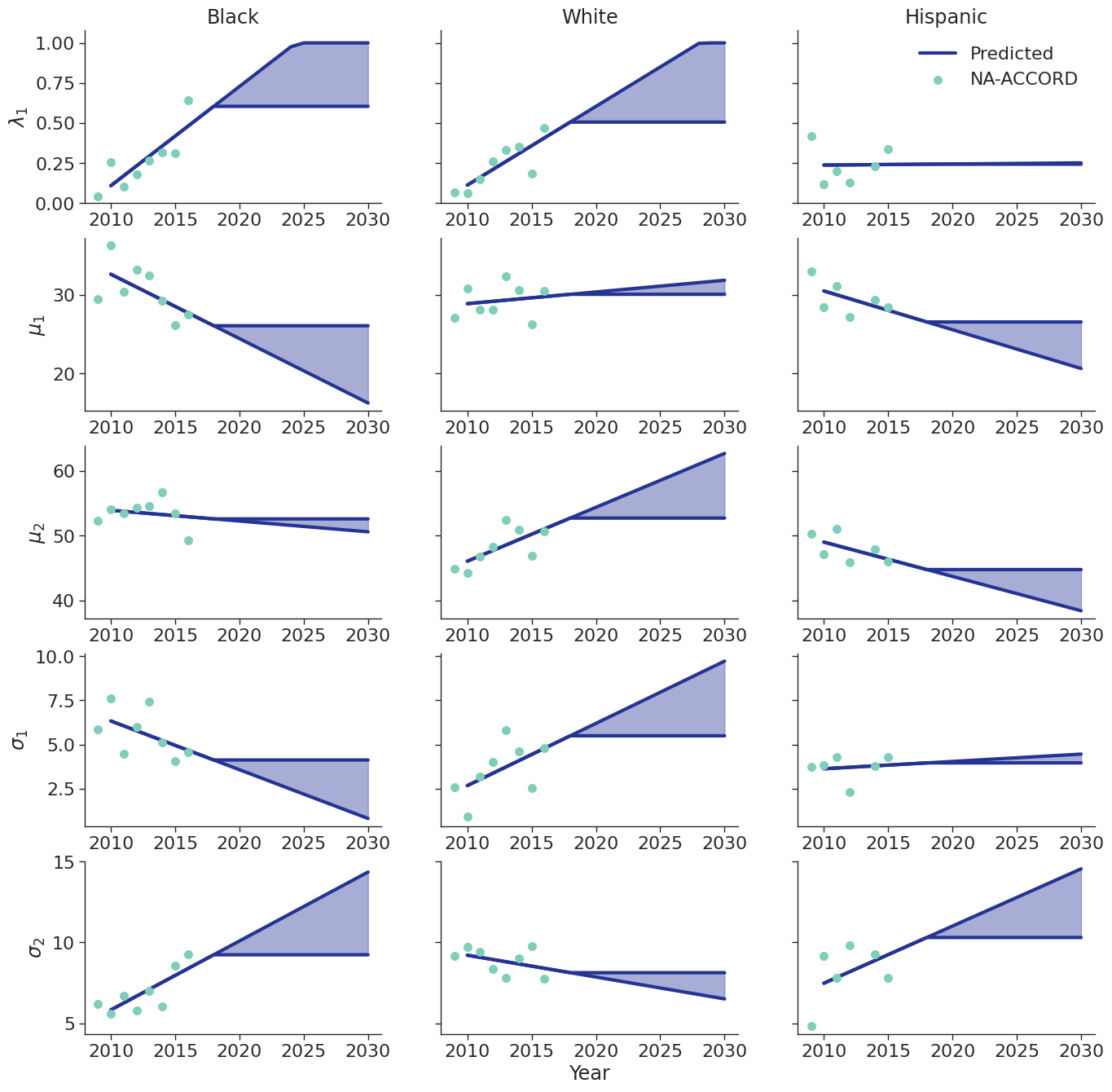
Figure 6e: MSM
CD4 Count at ART Initiation
Using data from NA-ACCORD, we categorized each sub-populations 8 categories based on ART initiation year (2010 – 2017). A normal distribution was fit to square root of CD4 count values for each sub-group and in each year. Within each sub-population, a linear regression model was applied to describe changes in the normal distribution parameters ($\mu$ mean and $\sigma$ standard deviation) over time, such that:
\[\mu(\mathrm{year}) = \mu_0 + \beta_\mu \cdot \mathrm{year}\]and
\[\sigma(\mathrm{year}) = \sigma_0 + \beta_\sigma \cdot \mathrm{year}\]Some sub-populations had to be collapsed by year in order to generate enough data for the regression as shown in the following figure:
Figure 7: CD4 Count Data Collapse
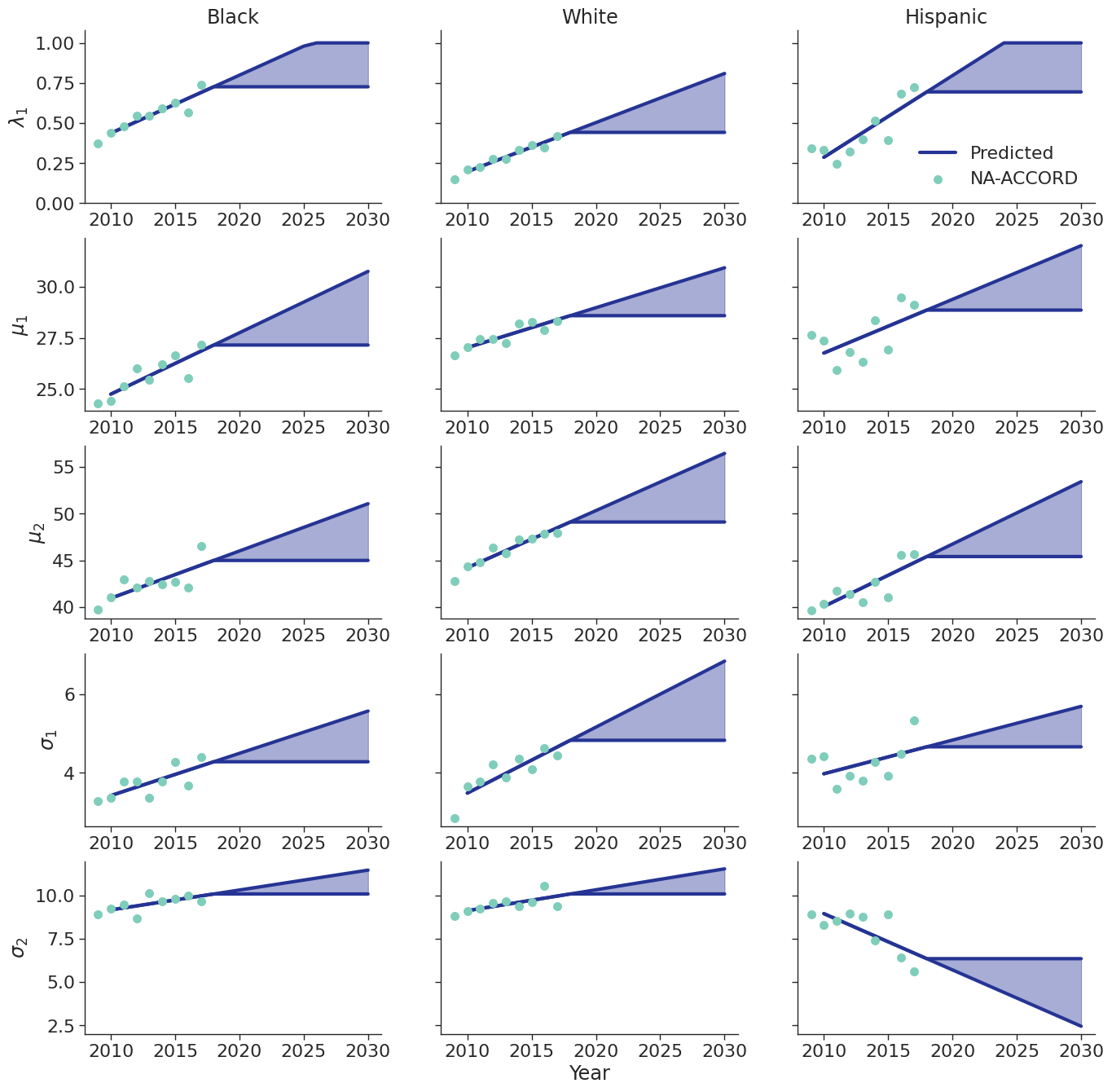
The fits were estimated using the glm function of the stats package in base R. Table 7 presents the value of the fitted coefficients and the trend is shown in Figure 8.
Table 7: ART Initiator Population CD4 Count Coefficients
When drawing CD4 values, we truncate the normal distribution at $0$ and $\sqrt{2000}$. Additionally, the predicted values in year 2018 were used as an upper/lower bound to develop a prediction range for future year.
Figure 8a: HET Female
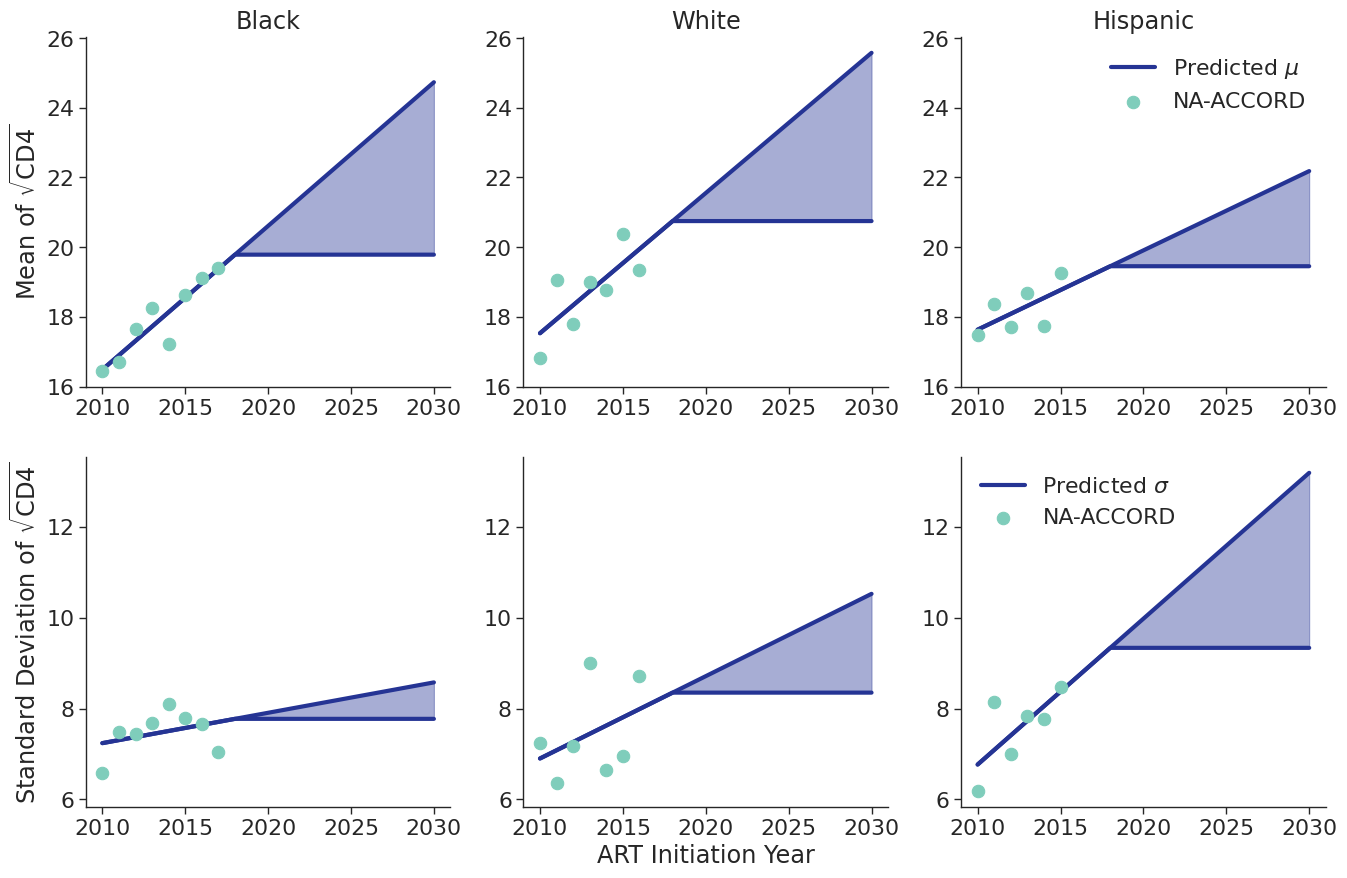
Figure 8b: HET Male
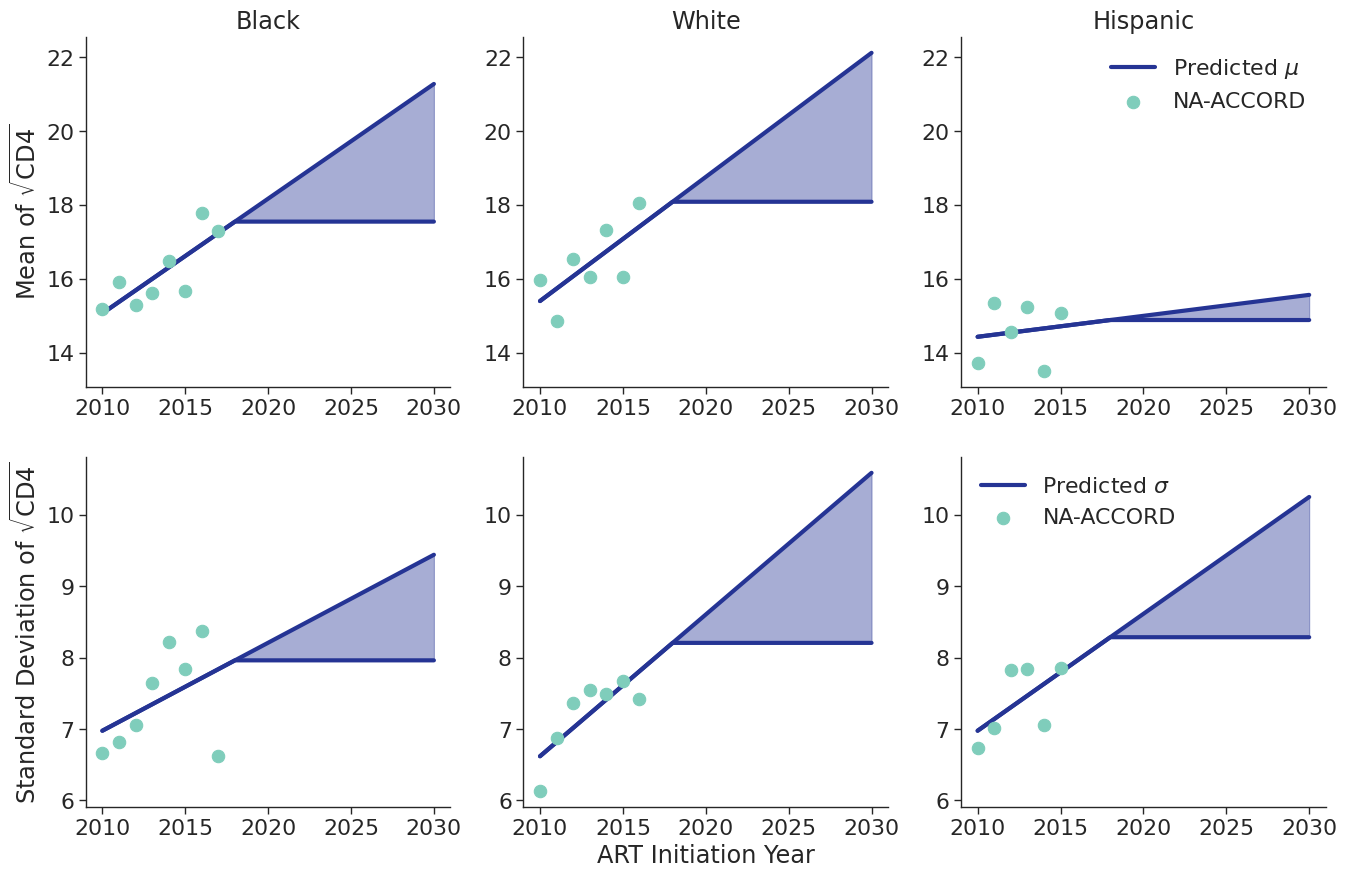
Figure 8c: IDU Female
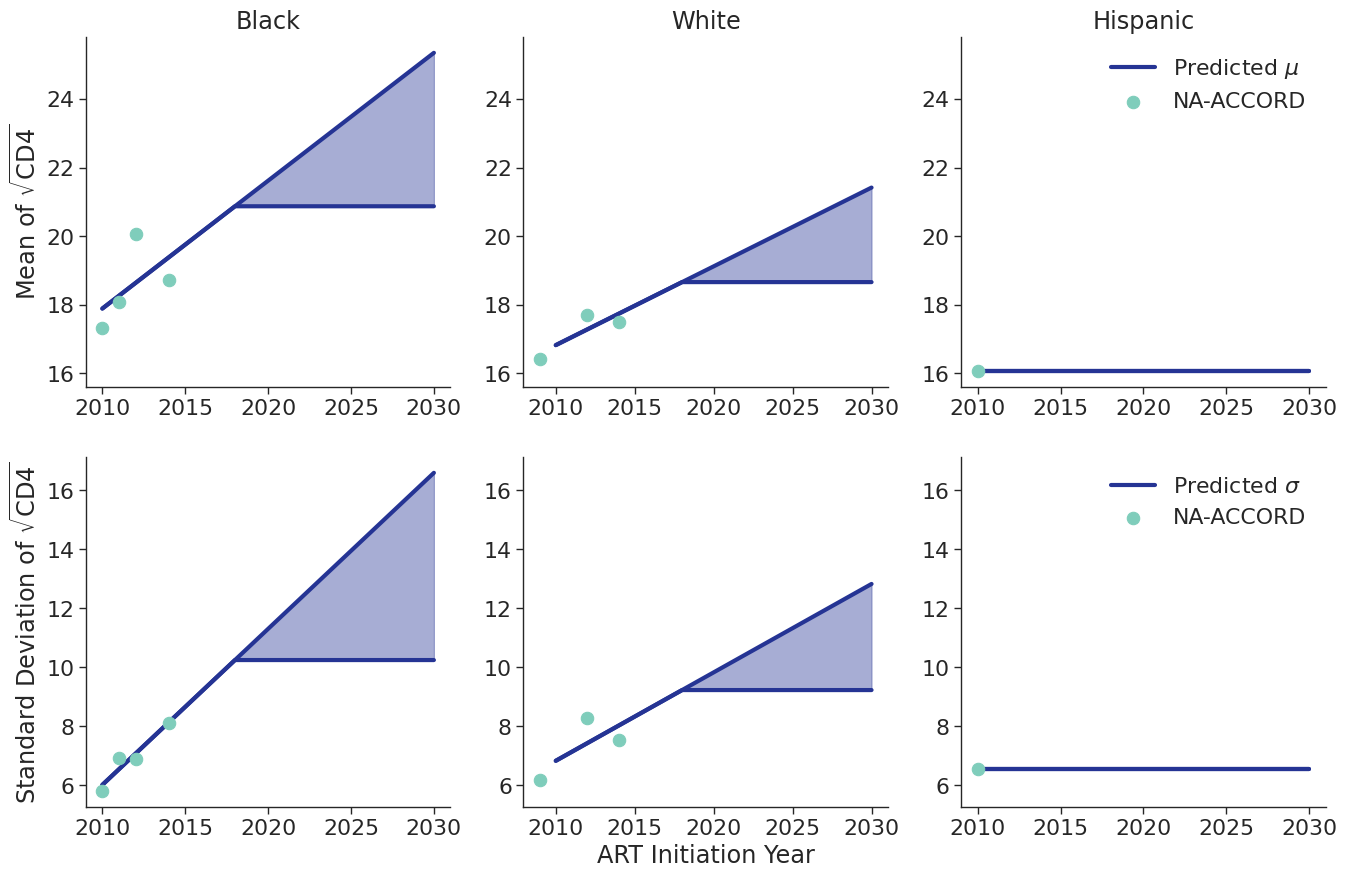
Figure 8d: IDU Male
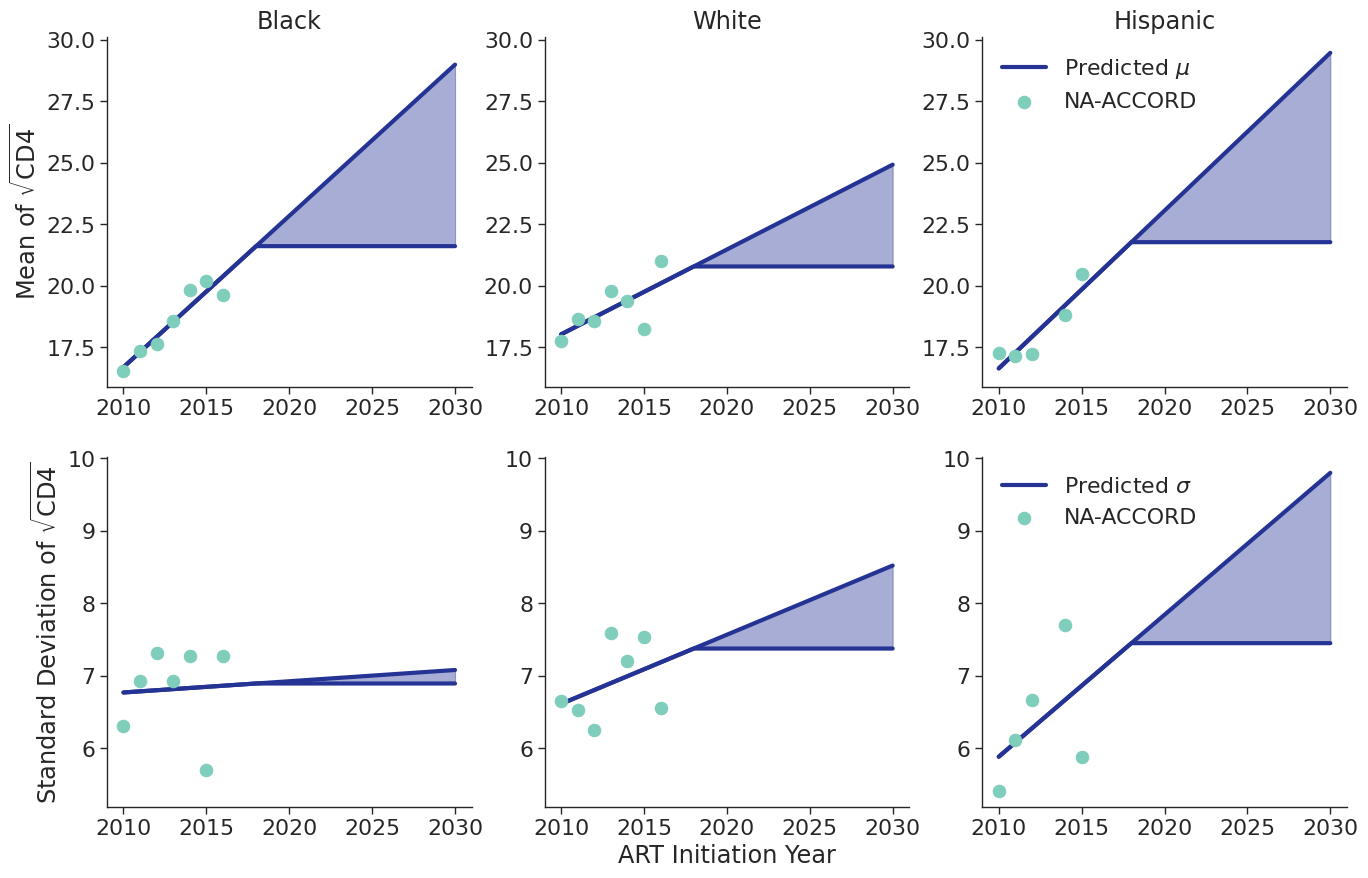
Figure 8e: MSM
Annual Population Dynamics
Disengagement From HIV Care
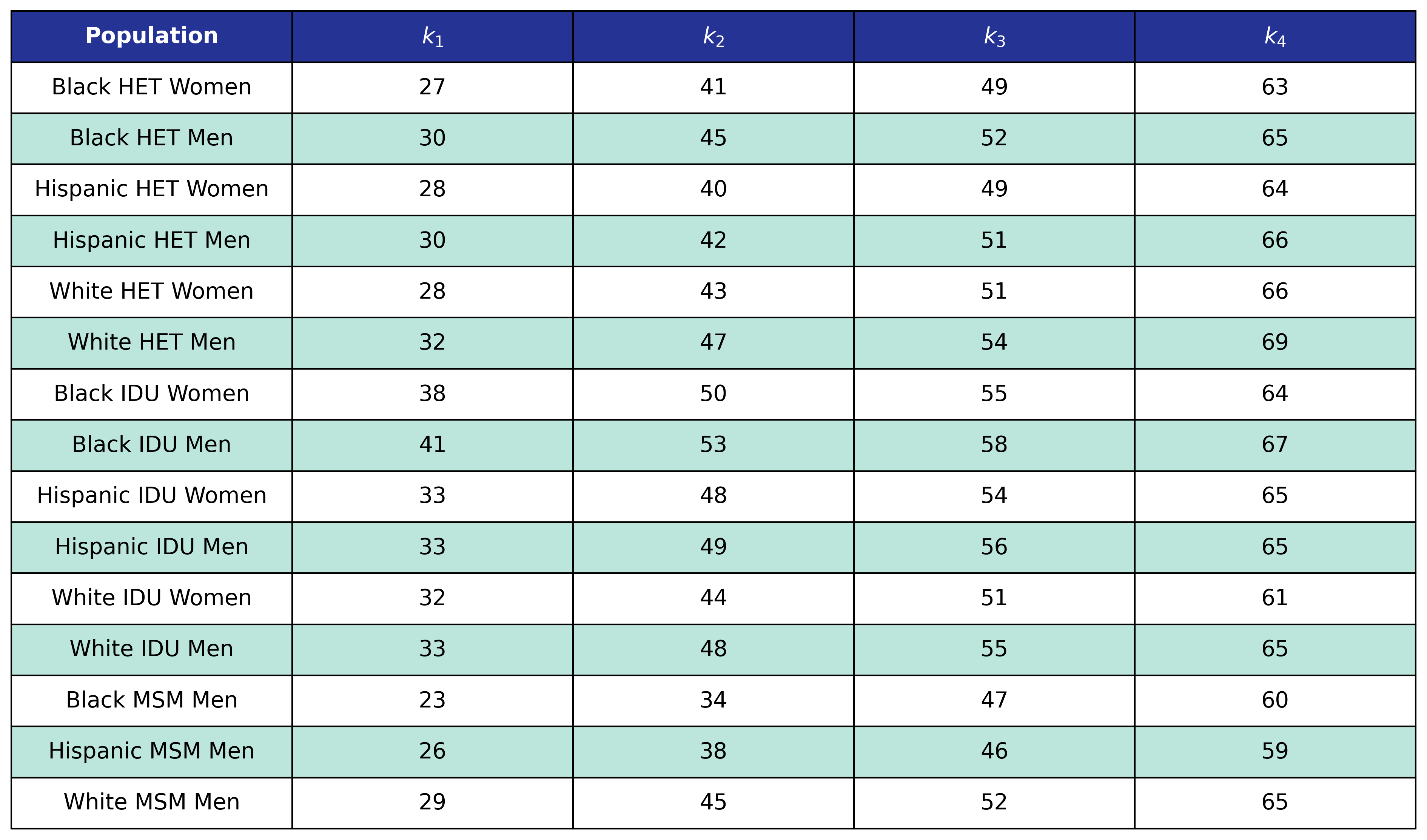
The NA-ACCORD dataset was restricted to the years 2009 – 2017 and each patient was represented by a data point for each year they were alive and under observation in NA-ACCORD. A patient was defined to be disengaged if ≥2 years had elapsed without a CD4 or viral load lab result and the year of disengagement was set to the first year without a lab. Using this data, a logistic regression was used to model the probability of disengagement as a function of calendar year ($\mathrm{year}$), square root of CD4 count at ART initiation (\(\mathrm{sqrt\_init\_cd4}\)), ART initiation period (\(\mathrm{art\_period}\)), and age ($\mathrm{age}$). ART initiation period was coded as a binary variable such that \(\mathrm{art\_period} = 1\) if ART was initiated after 2010 and 0 otherwise. Age is modeled as a restricted quadratic spline with 4 knots. The knots were placed at the 0.05, 0.35, 0.65, and 0.95 quantiles of the $\mathrm{age}$ variable (Table 8). The knot variables are defined such that
\[\mathrm{age}\_1 = \begin{cases} \frac{(\mathrm{age} - k_1)^2 - (\mathrm{age} - k_4)^2}{k_4 - k_1}, & \mathrm{age} \ge k_4\\ \frac{(\mathrm{age} - k_1)^2} {k_4 - k_1}, & k_4 \gt \mathrm{age} \ge k_1\\ 0, & \mathrm{else} \end{cases}\] \[\mathrm{age}\_2 = \begin{cases} \frac{(\mathrm{age} - k_2)^2 - (\mathrm{age} - k_4)^2}{k_4 - k_1}, & \mathrm{age} \ge k_4\\ \frac{(\mathrm{age} - k_2)^2} {k_4 - k_1}, & k_4 \gt \mathrm{age} \ge k_2\\ 0, & \mathrm{else} \end{cases}\] \[\mathrm{age}\_3 = \begin{cases} \frac{(\mathrm{age} - k_3)^2 - (\mathrm{age} - k_4)^2}{k_4 - k_1}, & \mathrm{age} \ge k_4\\ \frac{(\mathrm{age} - k_3)^2} {k_4 - k_1}, & k_4 \gt \mathrm{age} \ge k_3\\ 0, & \mathrm{else} \end{cases}\]Table 8: Disengagement Spline Knot Locations
The resulting regression equation is
\[\begin{split} \mathrm{logit}(p) = \beta_0 &+ \beta_\mathrm{year} \cdot\mathrm{year} + \beta_\mathrm{sqrt\_init\_cd4} \cdot\mathrm{sqrt\_init\_cd4} + \beta_\mathrm{art\_period} \cdot \mathrm{art\_period} \\[2ex] &+ \beta_\mathrm{age} \cdot\mathrm{age} + \beta_\mathrm{age\_1} \cdot\mathrm{age\_1} + \beta_\mathrm{age\_2} \cdot\mathrm{age\_2} + \beta_\mathrm{age\_3} \cdot\mathrm{age\_3} \end{split}\]where
\[\mathrm{logit}(p) = \log \frac{p}{1 - p}\]is the logit function and $p$ is the probability of disengagement from HIV care.
The coefficients were estimated using a generalized estimating equation (GEE) with a logit link and an exchangeable correlation structure using the geeglm function of the geepack software package for R. The estimated regression coefficients are shown in Table 9 and the covariance matrices is shown in Table 10.
Table 9: Disengagement Coefficient Estimates
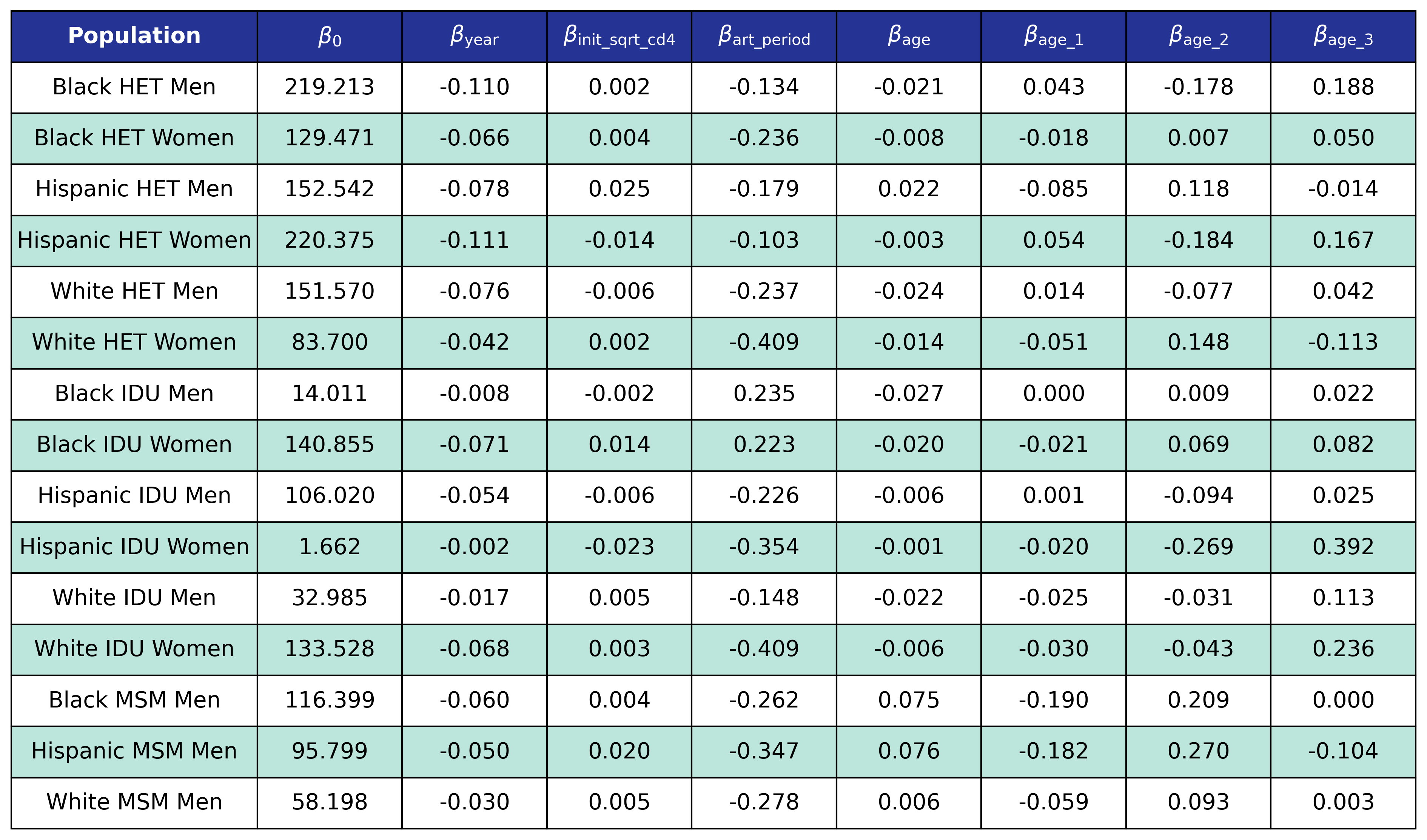
Table 10a: HET Female
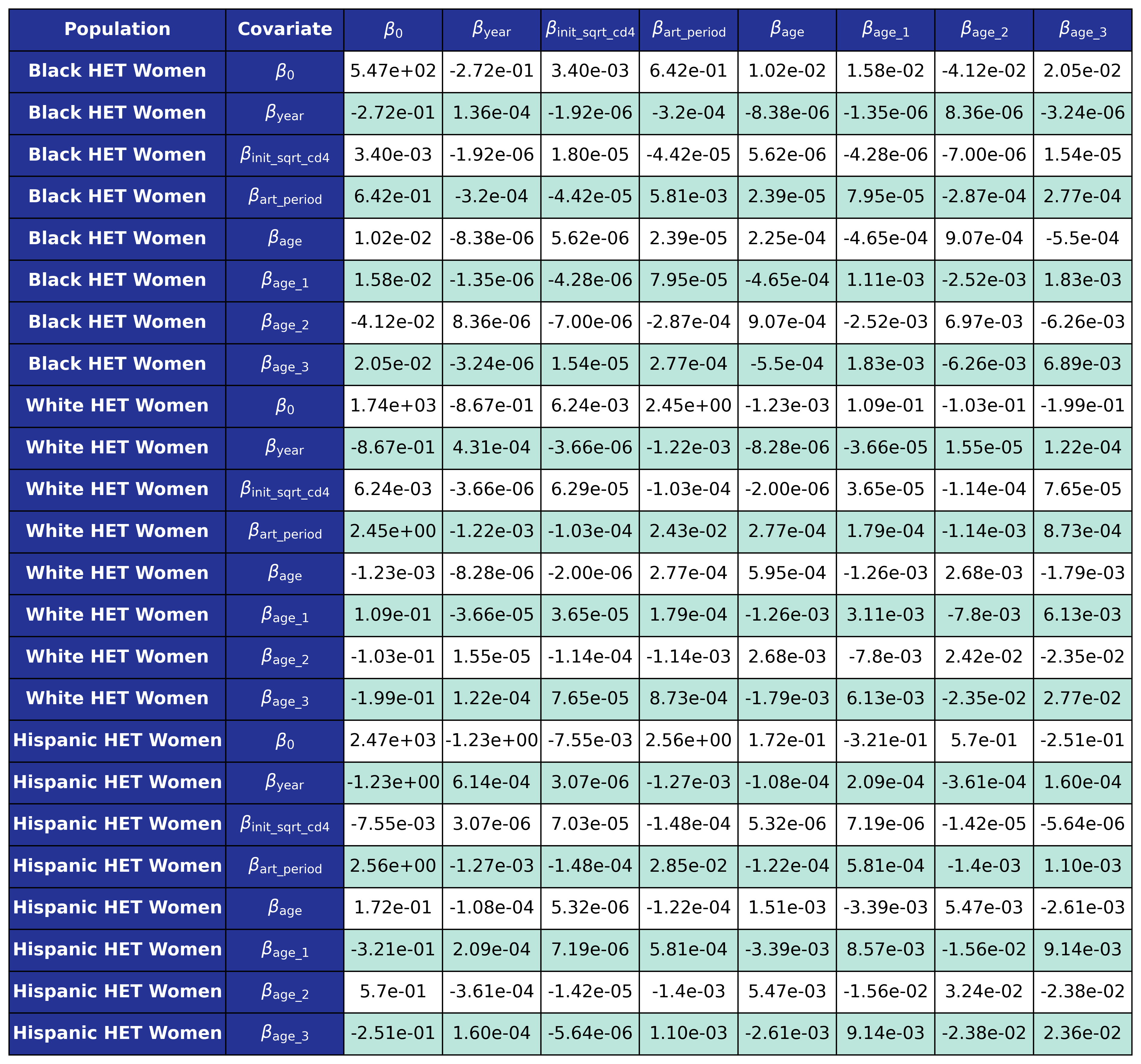
Table 10b: HET Male
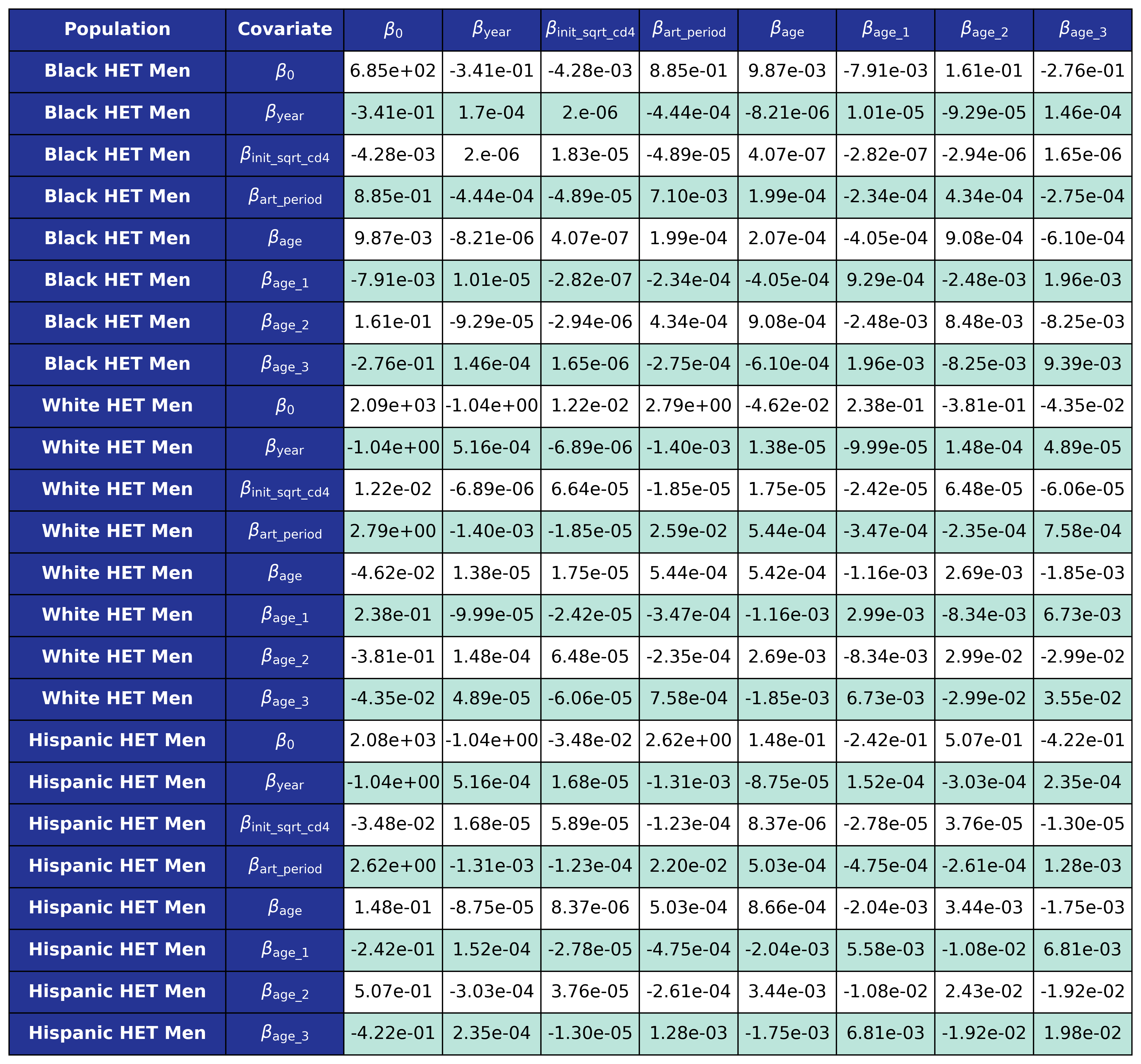
Table 10c: IDU Female
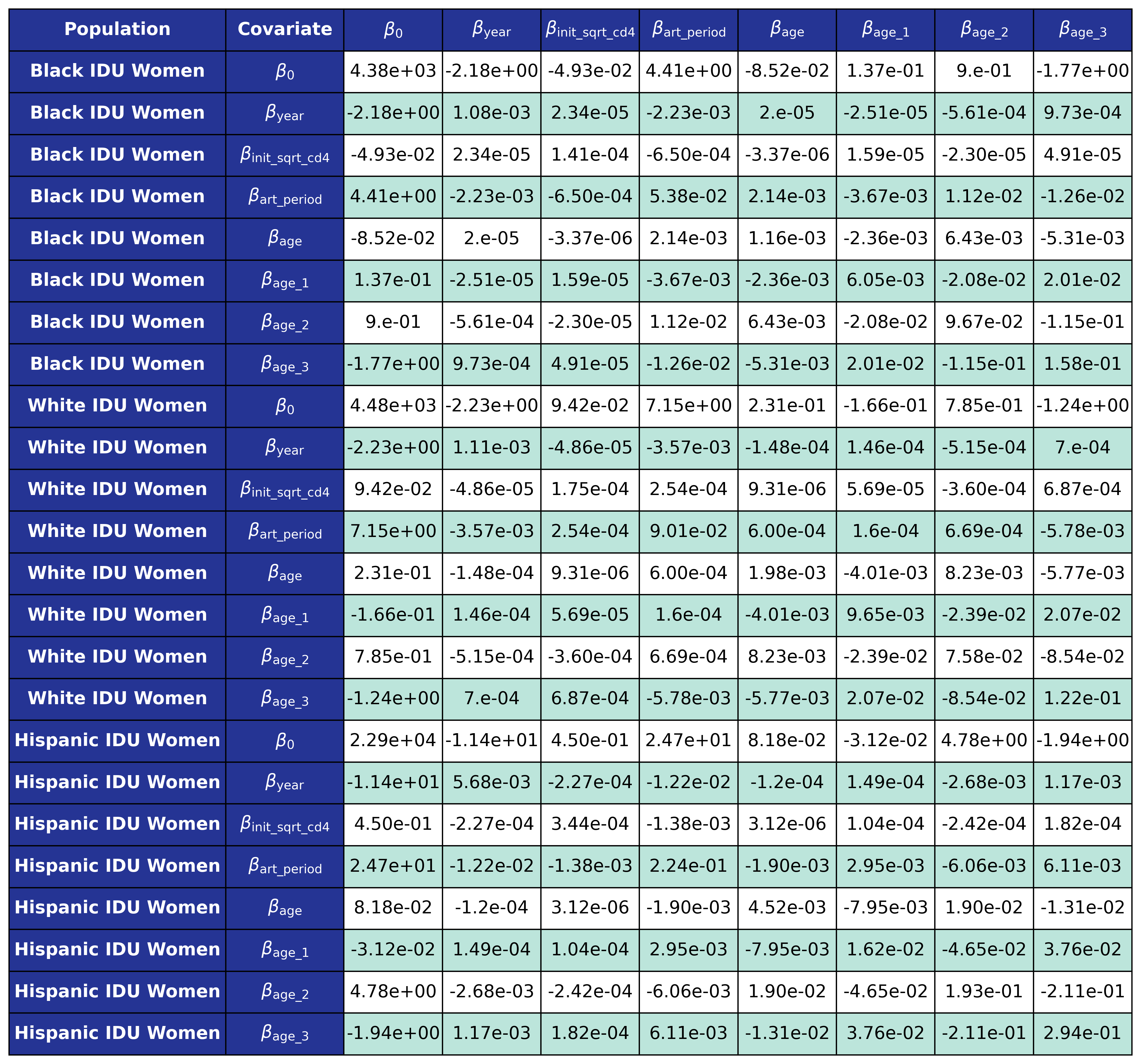
Table 10d: IDU Male
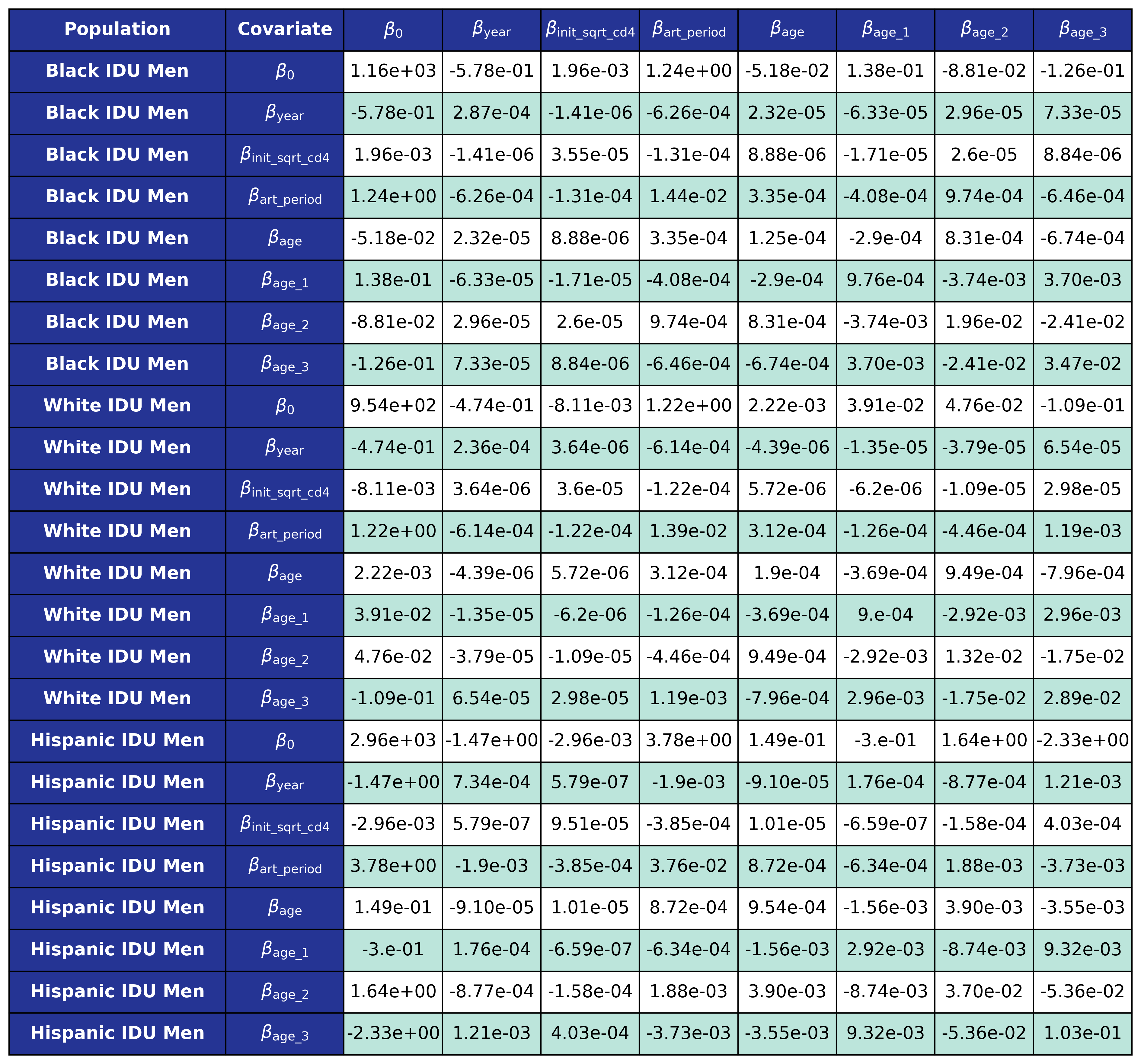
Table 10e: MSM
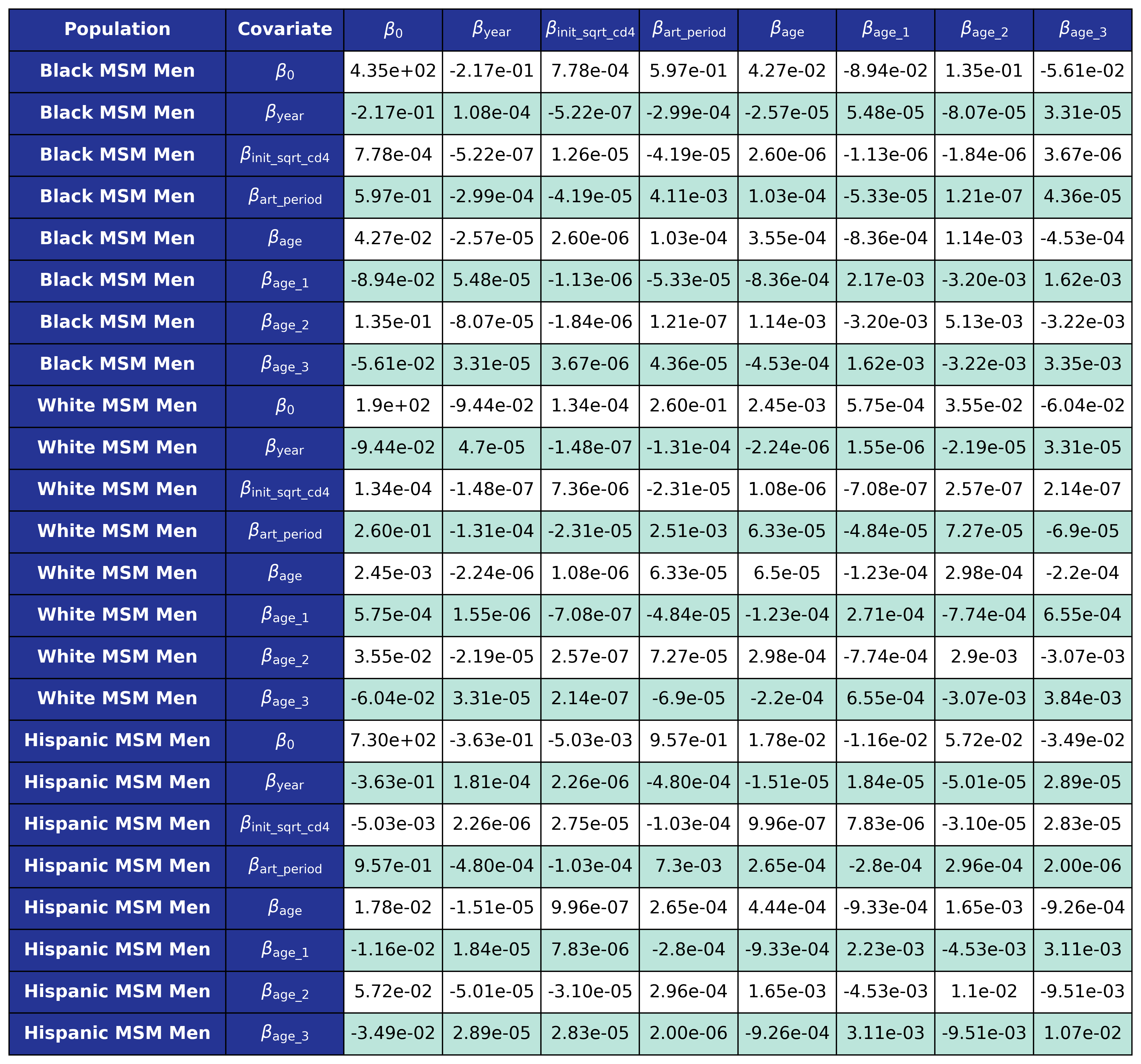
Reengagement With HIV Care
In order to model reengagement in care, we aggregated all sub-populations in the NA-ACCORD and assessed at the number of years spent out of care, estimated between 1 to 7 years. The probability of spending a certain number of years out of care was fit to a normalized Poisson distribution such that the probability of staying disengaged for more than 7 years was zero (Figure 7). The fit was accomplished using the curve_fit and poisson functions of the scipy package for Python. Upon disengagement, this distribution is applied to generate the number of years that a simulated person will spend off ART before reengaging back with treatment.
Figure 7: Number of Years Spent Out of Care
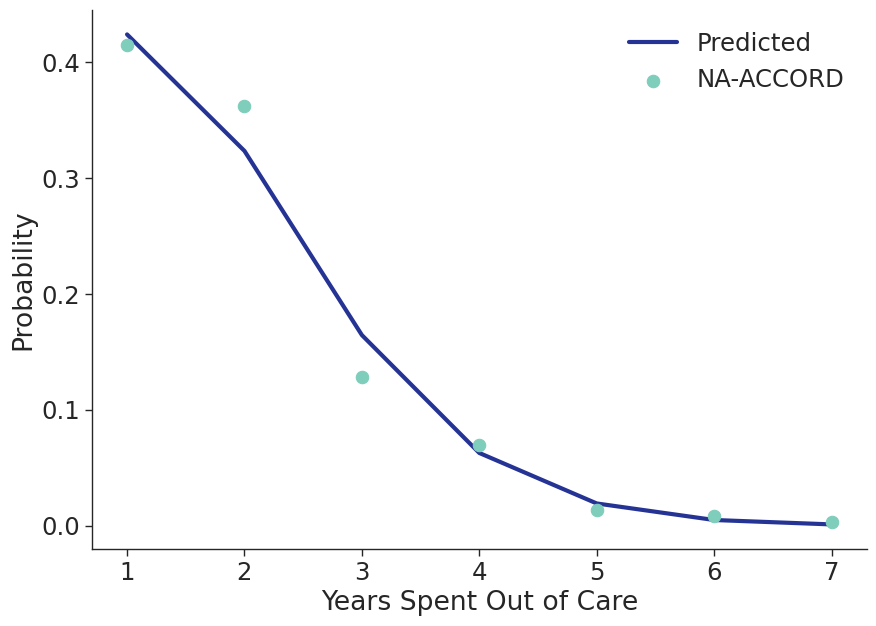
When simulated agents are lost to follow up, a number of years out of care is drawn from this distribution and the person will stay lost to follow up until they have spent the correct number of years out of care, they die, or the simulation ends.
Mortality In HIV Care
We constructed a sample of NA-ACCORD participants receiving ART between 2009–2017, and followed individuals from entry (set as maximum of ART initiation year and 2009) to exit (set as minimum of cohort close date, two years after the last lab result, and death year). Each participant was represented by a data point for each year that they were alive and under observation. A logistic regression was applied to model the probability of mortality as a linear function of calendar year (\(\mathrm{year}\)), \(\mathrm{age}\) and CD4 count at ART initiation (\(\mathrm{sqrt\_init\_cd4}\)) modeled as restricted cubic splines and year of ART initiation (\(\mathrm{art\_init\_year}\)) modeled categorically such that:
\[\mathrm{art\_init\_year\_1\ =\ }\left\{\begin{matrix}1,&2009\le\ \mathrm{art\_init\_year\ \le\ \ } 2012\mathrm{\ } \\0,&\mathrm{else},\\\end{matrix}\right.\] \[\mathrm{art\_init\_year\_2\ =\ }\left\{\begin{matrix}1,& \mathrm{art\_init\_year\ \ } \ge 2013 \\0,&\mathrm{else}.\\\end{matrix}\right.\]The full logistic regression equation is
\[\begin{split} \mathrm{logit}(p) = \beta_0 &+ \beta_\mathrm{year} \cdot\mathrm{year} + \beta_\mathrm{age} \cdot \mathrm{age} + \beta_\mathrm{age\_1} \cdot \mathrm{age\_1} + \beta_\mathrm{age\_2} \cdot \mathrm{age\_2} + \beta_\mathrm{sqrt\_init\_cd4}\cdot\mathrm{sqrt\_init\_cd4}\\[2ex] &+ \beta_\mathrm{sqrt\_init\_cd4\_1}\cdot\mathrm{sqrt\_init\_cd4\_1} + \beta_\mathrm{sqrt\_init\_cd4\_2}\cdot\mathrm{sqrt\_init\_cd4\_2}\\[2ex] &+ \beta_\mathrm{art\_init\_year\_1} \cdot \mathrm{art\_init\_year\_1}+ \beta_\mathrm{art\_init\_year\_2} \cdot \mathrm{art\_init\_year\_2} \end{split}\]where
\[\mathrm{logit}(p) = \log \frac{p}{1 - p}\]is the logit function and \(p\) is probability of dying in care. These coefficients were estimated using a GEE with a logit link and an exchangeable correlation structure using the geeglm function of the geepack software package for R. The NA-ACCORD dataset was restricted to the years 2009-2017 and each patient was represented by a data point for each year they were alive and under observation in NA-ACCORD. A mortality threshold was implemented such that for a given race, sex, and 5-year age category the overall probability of mortality must be greater that or equal to the annual mortality rate of the general population with the same characteristics as reported by the CDC. If the average probability was lower than this threshold, then the difference was added to each agent so that the distribution would be shifted to one with the same mean as the general population. The threshold was taken to be twice as high for IDU populations. The estimated regression coefficients and spline knots are shown in the following tables.
Table 11: Mortality In Care Coefficient Estimates
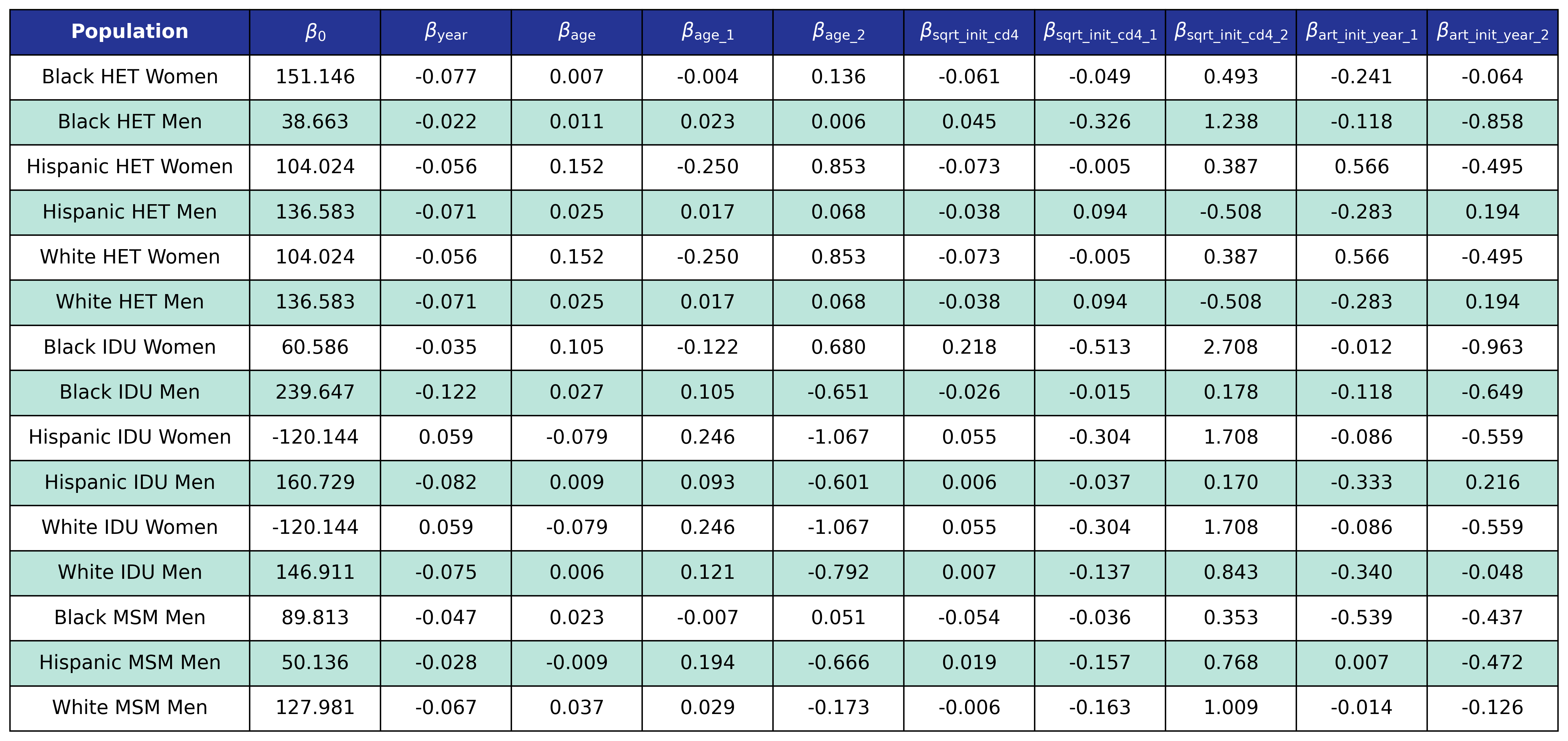
Table 12a: Mortality In Care Age Knots
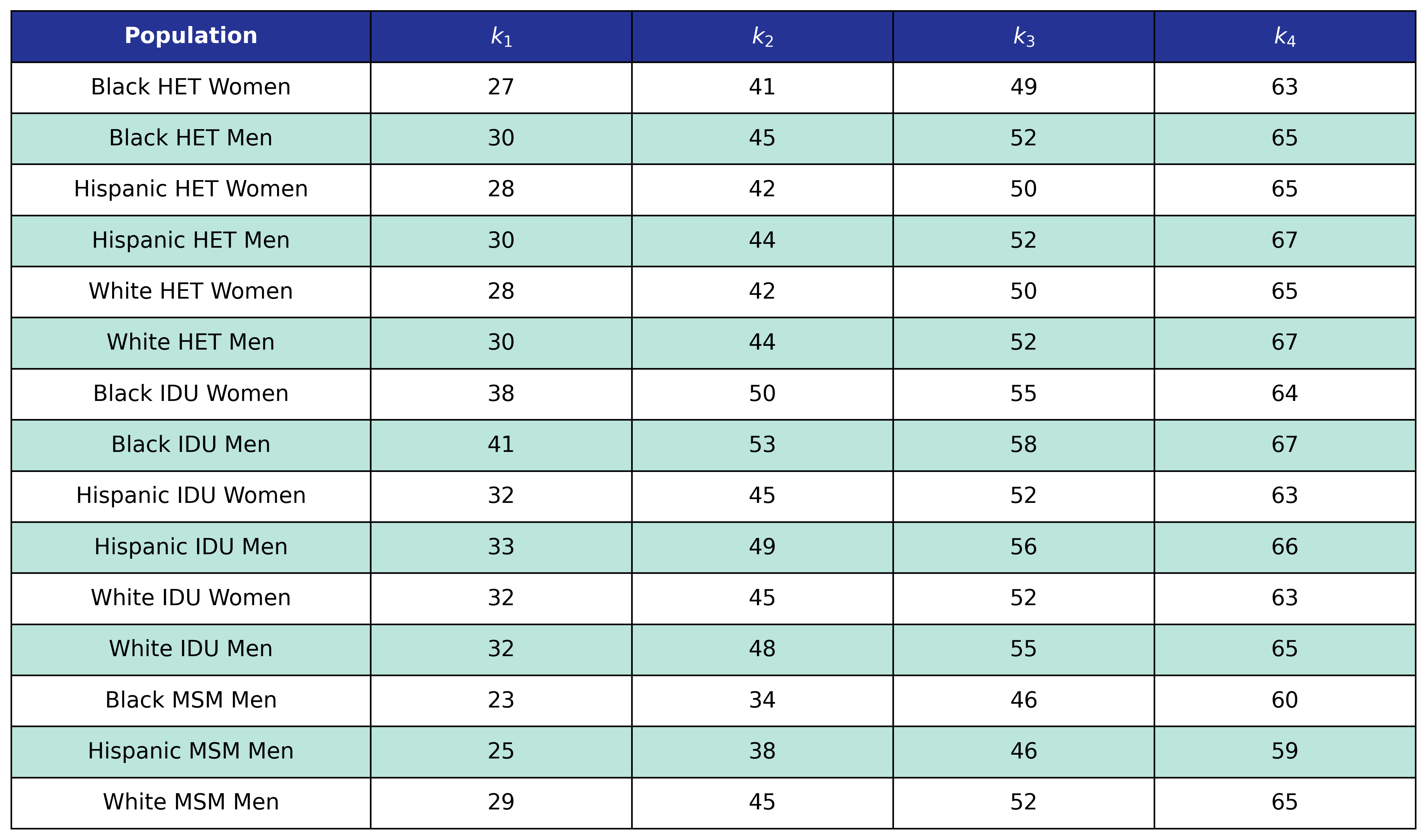
Table 12b: Mortality In Care CD4 Count Knots
Mortality out of HIV Care
Using reports of death for NA-ACCORD participants who were off ART at the time of death, a logistic regression was applied to model the probability of dying out of care as a linear function of calendar year (\(\mathrm{year}\)) and age (\(\mathrm{age}\)) and time-varying CD4 count (\(\mathrm{sqrt\_cd4}\)) modeled as restricted cubic splines such that:
\[\begin{split} \mathrm{logit}(p) = \beta_0 &+ \beta_\mathrm{year} \cdot\mathrm{year} + \beta_\mathrm{age} \cdot \mathrm{age} + \beta_\mathrm{age\_1} \cdot \mathrm{age\_1} + \beta_\mathrm{age\_2} \cdot \mathrm{age\_2} + \beta_\mathrm{sqrt\_cd4}\cdot\mathrm{sqrt\_cd4}\\[2ex] &+ \beta_\mathrm{sqrt\_cd4\_1}\cdot\mathrm{sqrt\_cd4\_1} + \beta_\mathrm{sqrt\_cd4\_2}\cdot\mathrm{sqrt\_cd4\_2} \end{split}\]where
\[\mathrm{logit}(p) = \log \frac{p}{1 - p}\]is the logit function and \(p\) is the probability of dying out of care. The coefficients were estimated using a GEE with a logit link and an exchangeable correlation structure using the geeglm function of the geepack software package for R. The NA-ACCORD dataset was restricted to the years 2009 – 2017. Each patient was represented by a data point for each year they were alive and out of care. The same mortality threshold was used for the out of care population as for the in care population. The estimated regression coefficients are shown in Table 13 and the covariance matrices are shown in Table 14.
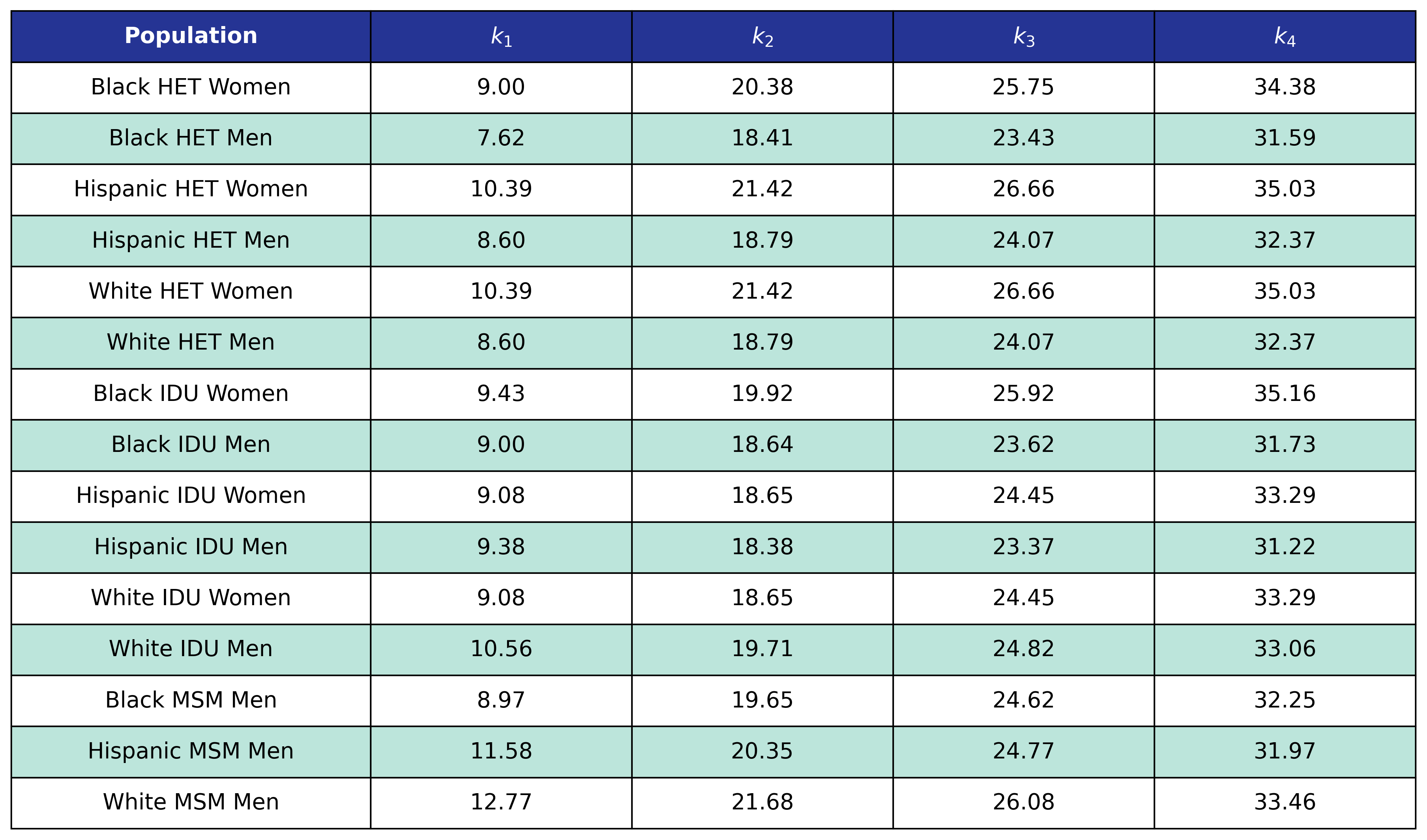
Table 13: Mortality Out of Care Coefficient Estimates
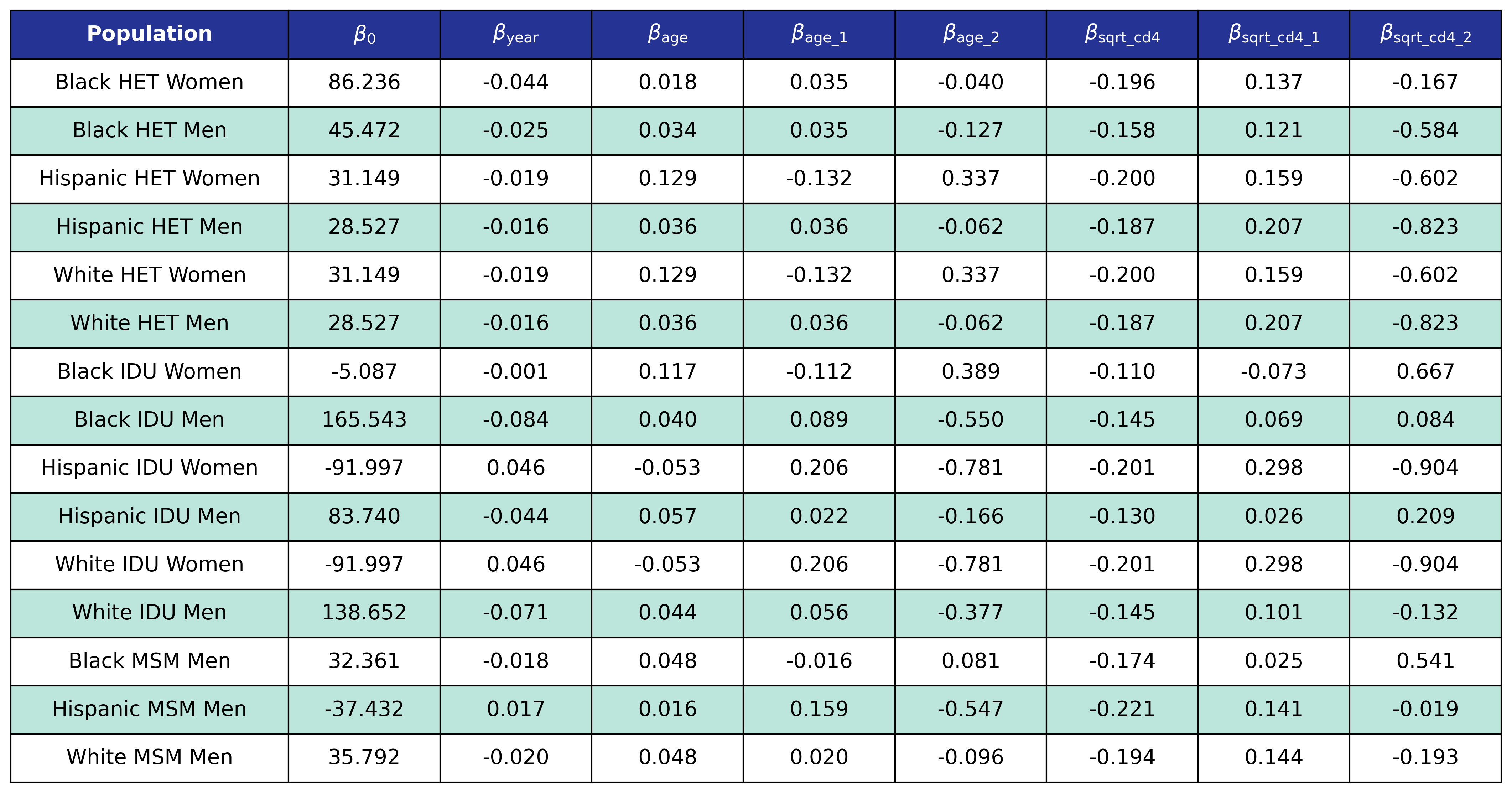
Table 14a: Mortality Out of Care Age Knots
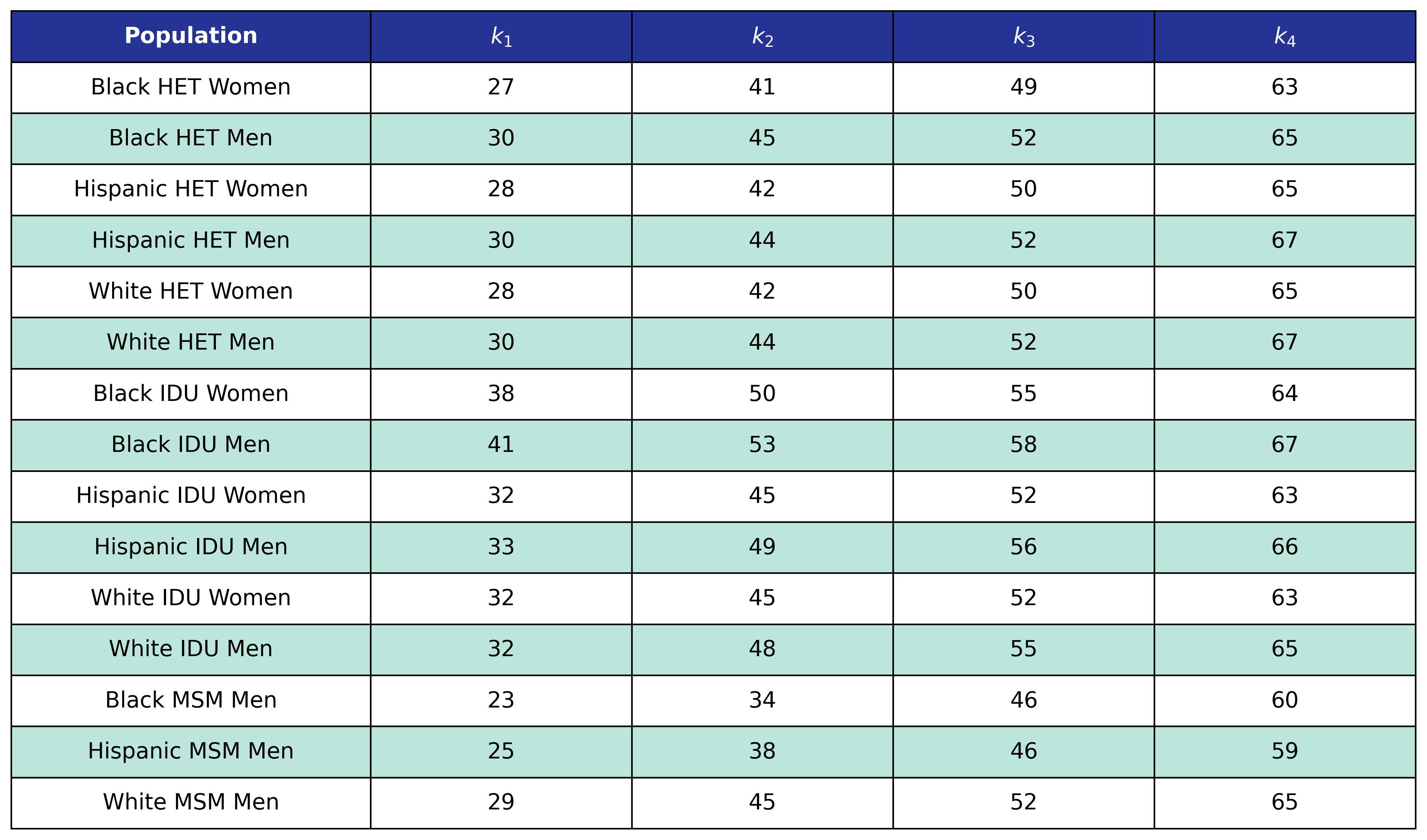
Table 14b: Mortality Out of Care CD4 Count Knots
CD4 Dynamics In Care
A linear regression was used to model the time varying CD4 count of those on ART. To this end, the square root of the time-varying CD4 count (\(\mathrm{sqrt\_cd4n}\)) was modeled as a linear function of 10 year age category (\(\mathrm{age\_cat}\)), square root of CD4 count at ART initiation (\(\mathrm{sqrt\_init\_cd4}\)), number of years since ART initiation (\(\mathrm{yrs\_art}\)), and interaction terms between CD4 count at ART initiation and number of years since ART initiation. The square root of CD4 count at ART initiation is represented by three binary variables such that
\[\mathrm{cd4\_cat\_1\ =\ }\left\{\begin{matrix}1,&\sqrt{200}\le\ \mathrm{sqrt\_init\_cd4\ \le\ \ } \sqrt{350}\mathrm{\ } \\0,&\mathrm{else},\\\end{matrix}\right.\] \[\mathrm{cd4\_cat\_2\ =\ }\left\{\begin{matrix}1,&\sqrt{350}\le\ \mathrm{sqrt\_init\_cd4\ \le\ \ } \sqrt{500}\mathrm{\ } \\0,&\mathrm{else},\\\end{matrix}\right.\]and
\[\mathrm{cd4\_cat\_3\ =\ }\left\{\begin{matrix}1,&\sqrt{500}\le\ \mathrm{sqrt\_init\_cd4\ \ } \\0,&\mathrm{else}.\\\end{matrix}\right.\]The number of years since ART initiation is modeled as a restricted quadratic spline with 4 knots:
\[\mathrm{yrs\_art}\_1 = \begin{cases} \frac{(\mathrm{yrs\_art} - k_1)^2 - (\mathrm{yrs\_art} - k_4)^2}{k_4 - k_1}, & \mathrm{yrs\_art} \ge k_4\\ \frac{(\mathrm{yrs\_art} - k_1)^2} {k_4 - k_1}, & k_4 \gt \mathrm{yrs\_art} \ge k_1\\ 0, & \mathrm{else} \end{cases}\] \[\mathrm{yrs\_art}\_2 = \begin{cases} \frac{(\mathrm{yrs\_art} - k_2)^2 - (\mathrm{yrs\_art} - k_4)^2}{k_4 - k_1}, & \mathrm{yrs\_art} \ge k_4\\ \frac{(\mathrm{yrs\_art} - k_2)^2} {k_4 - k_1}, & k_4 \gt \mathrm{yrs\_art} \ge k_2\\ 0, & \mathrm{else} \end{cases}\] \[\mathrm{yrs\_art}\_3 = \begin{cases} \frac{(\mathrm{yrs\_art} - k_3)^2 - (\mathrm{yrs\_art} - k_4)^2}{k_4 - k_1}, & \mathrm{yrs\_art} \ge k_4\\ \frac{(\mathrm{yrs\_art} - k_3)^2} {k_4 - k_1}, & k_4 \gt \mathrm{yrs\_art} \ge k_3\\ 0, & \mathrm{else} \end{cases}\]The same knot locations were used for each population at $k_1=1$, $k_2=4$, $k_3=7$, and $k_4=13$. The final regression equation resulting from this choice of regressors are as follow:
\[\begin{split} \mathrm{sqrt\_cd4} = \beta_0 &+ \beta_\mathrm{age\_cat} \cdot\mathrm{age\_cat} + \beta_\mathrm{cd4\_cat\_1} \cdot\mathrm{cd4\_cat\_1} + \beta_\mathrm{cd4\_cat\_2} \cdot \mathrm{cd4\_cat\_2} + \beta_\mathrm{cd4\_cat\_3} \cdot \mathrm{cd4\_cat\_3}\\[2ex] &+ \beta_\mathrm{yrs\_art} \cdot \mathrm{yrs\_art} + \beta_\mathrm{yrs\_art\_1} \cdot \mathrm{yrs\_art\_1} + \beta_\mathrm{yrs\_art\_2} \cdot \mathrm{yrs\_art\_2} + \beta_\mathrm{yrs\_art\_3} \cdot \mathrm{yrs\_art\_3}\\[2ex] &+ \beta_\mathrm{cd4\_1\_yrs\_1} \cdot \mathrm{cd4\_cat\_1} \cdot \mathrm{yrs\_art\_1} + \beta_\mathrm{cd4\_1\_yrs\_2} \cdot \mathrm{cd4\_cat\_1} \cdot \mathrm{yrs\_art\_2}+ \beta_\mathrm{cd4\_1\_yrs\_3} \cdot \mathrm{cd4\_cat\_1} \cdot \mathrm{yrs\_art\_3}\\[2ex] &+ \beta_\mathrm{cd4\_2\_yrs\_1} \cdot \mathrm{cd4\_cat\_2} \cdot \mathrm{yrs\_art\_1} + \beta_\mathrm{cd4\_2\_yrs\_2} \cdot \mathrm{cd4\_cat\_2} \cdot \mathrm{yrs\_art\_2}+ \beta_\mathrm{cd4\_2\_yrs\_3} \cdot \mathrm{cd4\_cat\_2} \cdot \mathrm{yrs\_art\_3}\\[2ex] &+ \beta_\mathrm{cd4\_3\_yrs\_1} \cdot \mathrm{cd4\_cat\_3} \cdot \mathrm{yrs\_art\_1} + \beta_\mathrm{cd4\_3\_yrs\_2} \cdot \mathrm{cd4\_cat\_3} \cdot \mathrm{yrs\_art\_2}+ \beta_\mathrm{cd4\_3\_yrs\_3} \cdot \mathrm{cd4\_cat\_3} \cdot \mathrm{yrs\_art\_3} \end{split}\]The coefficients were estimated using a generalized estimating equation (GEE) with an identity link function and an exchangeable correlation structure. The NA-ACCORD population was filtered to those that never left care during study follow-up. Patients who initiated ART before 2000 and who were missing CD4 count data at ART initiation were dropped from analysis. Each remaining patient was assigned a single data point per year for the full range of years 2009 – 2017 and the CD4 count was taken to be the median CD4 count by calendar year. The resulted coefficient estimates are shown in Table 15 and the covariance matrices are shown in Table 16
Table 15: CD4 Increase Coefficient Estimates
CD4 Dynamics Out of Care
The decrease in CD4 count off ART was modeled using a linear regression scheme. NA-ACCORD participants that left care from 2010 – 2016 and returned 2011 – 2017 and had a valid CD4 measurement at entry and exit were used in the analysis. Patients whose CD4 count had increased or stayed the same as well as those who had a suppressed viral load on return were dropped as well. All sub-populations had to be collapsed in order to provide enough data. We assumed that the difference (\(\mathrm{diff\_log}\)) of the log of the entry CD4 count (\(\mathrm{sqrt\_cd4}^2\)) from the log of CD4 count at exit from care (\(\mathrm{sqrt\_cd4\_exit}^2\)) varies linearly with number of years spent out of care (\(\mathrm{years\_out}\)), and square root of CD4 count at exit from care (\(\mathrm{sqrt\_cd4\_exit}\)):
\[\mathrm{diff\_log} = \beta_0 + \beta_\mathrm{years\_out} \cdot \mathrm{years\_out} + \beta_\mathrm{sqrt\_cd4\_exit} \cdot \mathrm{sqrt\_cd4\_exit}\]where
\[\mathrm{diff\_log} = \log(\mathrm{sqrt\_cd4}^2) - \log(\mathrm{sqrt\_cd4\_exit}^2)\]The variable of interest is the time varying CD4 count (\(\mathrm{cd4\_entry}\)). Solving for \(\mathrm{sqrt\_cd4}\) leaves us with
\[\mathrm{sqrt\_cd4} = (c_s \cdot e^{\mathrm{diff\_log}}\cdot \mathrm{sqrt\_cd4\_exit}^2)^\frac{1}{2}\]where \(c_s = 1.4\) is the smearing retransformation term resulting from fitting a linear regression to a log-transformed variable. The fit was performed using the glm function of the stats package in base R. The estimated coefficients are shown in Table 17 and the covariance matrix is shown in Table 18.
Table 17: CD4 Out of Care Coefficient Estimates

Table 18: CD4 Out of Care Covariance Matrix

Multimorbidity and BMI
The simulation may be run with or without the presence of comorbid conditions and BMI. The possible comorbid conditions are partitioned into multiple “stages” depending on how they are modeled in the simulation. Smoking and hepatitis C virus are risk factors, anxiety and depression are stage 1, chronic kidney disease, hyperlipidemia, diabetes mellitus, and hypertension are stage 2, and cancer, end-stage liver disease and myocardial infarction are stage 3. Incidence of conditions of a certain stage are influenced by presence of conditions from previous stages as well as other factors as detailed in the following. Mortality functions are modified to account for the comorbid conditions as well.
BMI
In order to capture the important clinical effect of change in BMI resulting from ART treatment, we model both pre-ART BMI and post-ART BMI for all agents. Both BMI measurements then have an effect on comorbid conditions and mortality.
Pre-ART BMI
Pre-ART BMI (\(\mathrm{pre\_art\_bmi}\)) is calculated from one of four different models depending on the subpopulation.
Model 1
Model 1 is used only by the \(\mathrm{idu\_hisp\_male}\) population. We model \(\log_{10}(\mathrm{pre\_art\_bmi})\) as a function of age category (\(\mathrm{age\_cat}\)) and \(\mathrm{art\_init\_year}\). The age categories are given by
\[\mathrm{age\_cat\_1\ =\ }\left\{\begin{matrix}1,&30\le\ \mathrm{age\ \le\ \ } 39\mathrm{\ } \\0,&\mathrm{else},\\\end{matrix}\right.\] \[\mathrm{age\_cat\_2\ =\ }\left\{\begin{matrix}1,&40\le\ \mathrm{age\ \le\ \ } 49\mathrm{\ } \\0,&\mathrm{else},\\\end{matrix}\right.\] \[\mathrm{age\_cat\_3\ =\ }\left\{\begin{matrix}1,&50\le\ \mathrm{age\ \le\ \ } 59\mathrm{\ } \\0,&\mathrm{else},\\\end{matrix}\right.\]and
\[\mathrm{age\_cat\_4\ =\ }\left\{\begin{matrix}1,&60\le\ \mathrm{age\ \ } \\0,&\mathrm{else}.\\\end{matrix}\right.\]A restricted cubic spline is used to model \(\mathrm{art\_init\_year}\) with the following knots:
Table 19: Pre-ART BMI Model 1 Knots

The full function is given by:
\[\begin{split} \log_{10}(\mathrm{pre\_art\_bmi}) = \beta_0 &+ \beta_\mathrm{age\_cat\_1} \cdot \mathrm{age\_cat\_1} + \beta_\mathrm{age\_cat\_2} \cdot \mathrm{age\_cat\_2} + \beta_\mathrm{age\_cat\_3} \cdot \mathrm{age\_cat\_3} + \beta_\mathrm{age\_cat\_4} \cdot \mathrm{age\_cat\_4}\\[2ex] &+ \beta_\mathrm{art\_init\_year} \cdot \mathrm{art\_init\_year}+ \beta_\mathrm{art\_init\_year\_1} \cdot \mathrm{art\_init\_year\_1} + \beta_\mathrm{art\_init\_year\_2} \cdot \mathrm{art\_init\_year\_2} \end{split}\]Table 20: Pre-ART BMI Model 1 Estimates
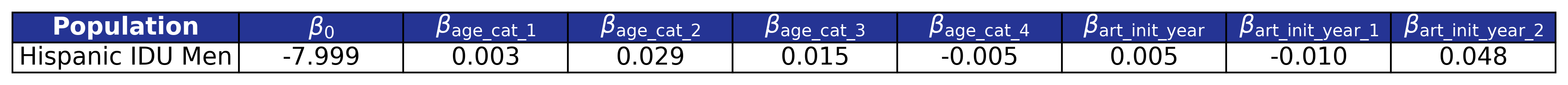
Model 2
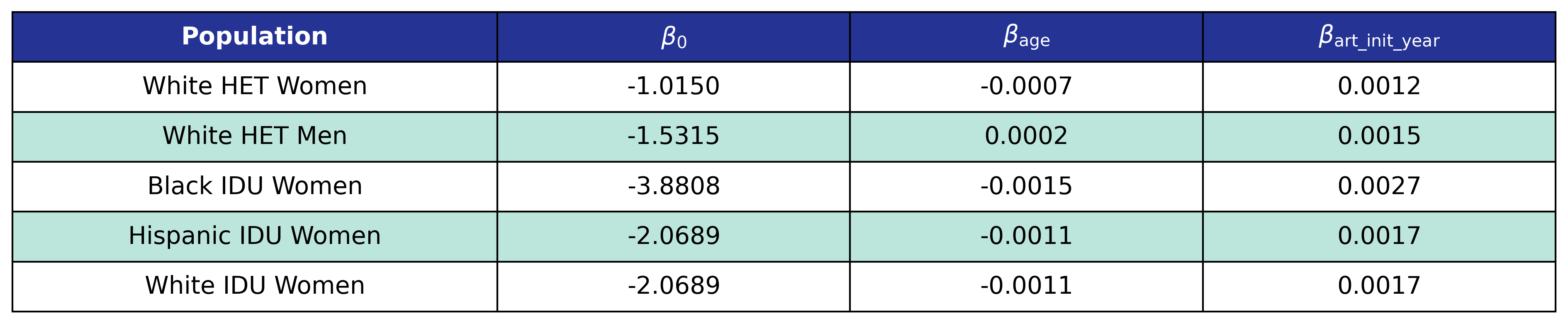
Model 2 is used by the \(\mathrm{het\_white\_female}\), \(\mathrm{het\_white\_male}\), \(\mathrm{idu\_black\_female}\), \(\mathrm{idu\_hisp\_female}\), and \(\mathrm{idu\_white\_female}\) populations. We model \(\log_{10}(\mathrm{pre\_art\_bmi})\) as a linear function of \(\mathrm{age}\) and \(\mathrm{art\_init\_year}\)
\[\log_{10}(\mathrm{pre\_art\_bmi}) = \beta_0 + \beta_\mathrm{age} \cdot \mathrm{age} + \beta_\mathrm{art\_init\_year} \cdot \mathrm{art\_init\_year}\]Table 21: Pre-ART BMI Model 2 Estimates
Model 3
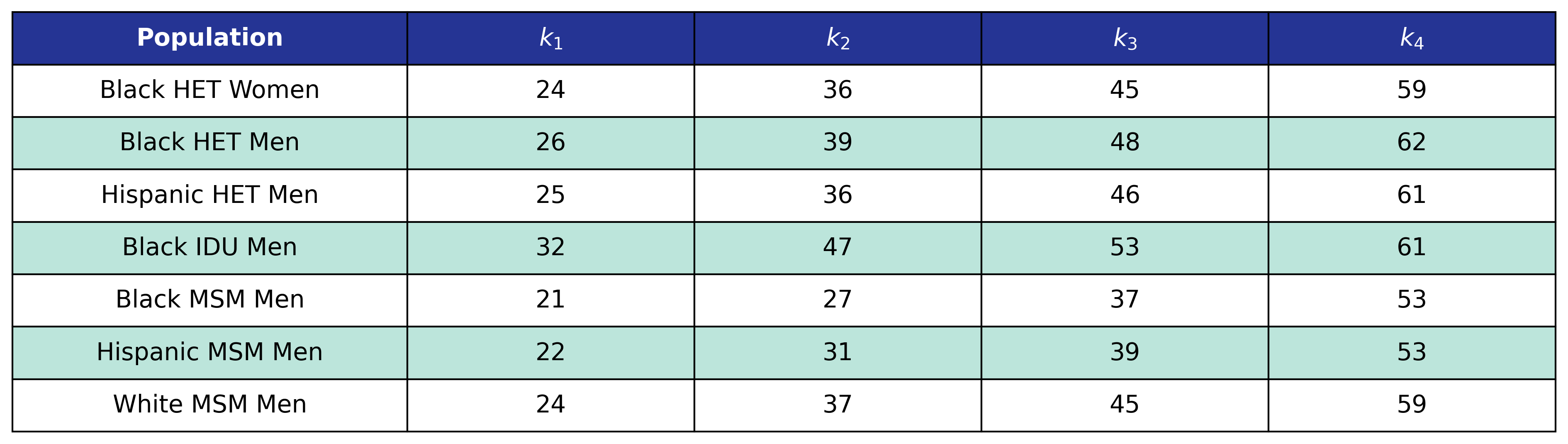
Model 3 is used by the \(\mathrm{het\_black\_female}\), \(\mathrm{het\_black\_male}\), \(\mathrm{het\_hisp\_male}\), \(\mathrm{idu\_black\_male}\), \(\mathrm{msm\_black\_male}\), \(\mathrm{msm\_hisp\_male}\), and \(\mathrm{msm\_white\_male}\) populations. We model \(\log_{10}(\mathrm{pre\_art\_bmi})\) as a restricted cubic spline function of \(\mathrm{age}\) and a linear function of \(\mathrm{art\_init\_year}\).
Table 22: Pre-ART BMI Model 3 Knots
The function and its estimates follow.
\[\log_{10}(\mathrm{pre\_art\_bmi}) = \beta_0 + \beta_\mathrm{age} \cdot \mathrm{age} + \beta_\mathrm{age\_1} \cdot \mathrm{age\_1} + \beta_\mathrm{age\_2} \cdot \mathrm{age\_2} + \beta_\mathrm{art\_init\_year} \cdot \mathrm{art\_init\_year}\]Table 23: Pre-ART BMI Model 3 Estimates
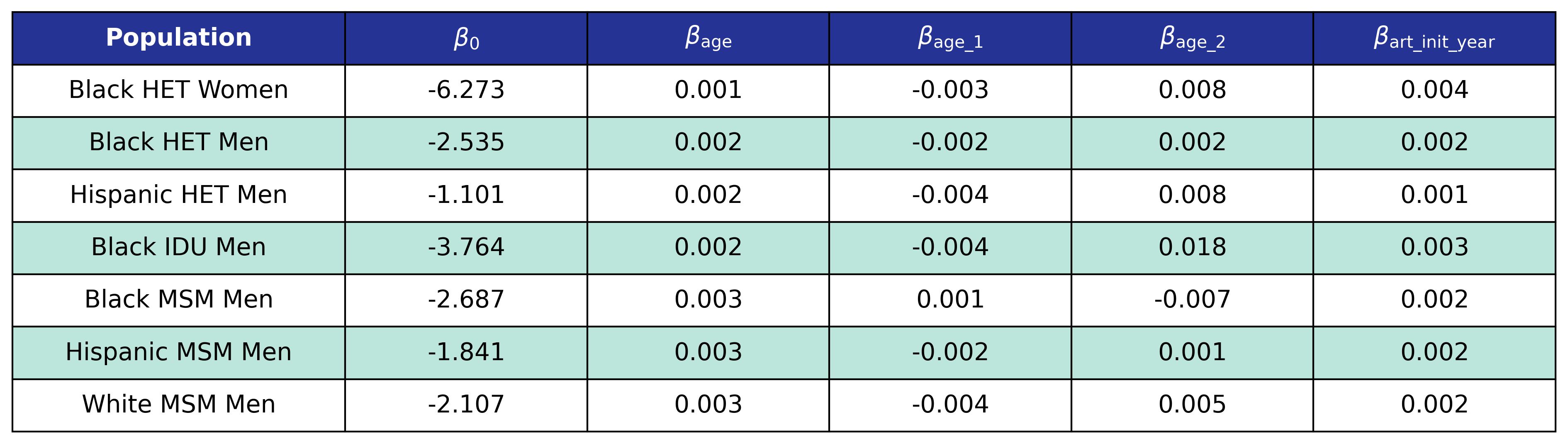
Model 4
Model 2 is used by the \(\mathrm{het\_hisp\_female}\) and \(\mathrm{idu\_white\_male}\) populations. We model \(\log_{10}(\mathrm{pre\_art\_bmi})\) as a restricted cubic spline function of age \(\mathrm{age}\) and \(\mathrm{art\_init\_year}\).
Table 24: Pre-ART BMI Model 4 Age Knots

Table 25: Pre-ART BMI Model 4 ART Initiation Year Knots

The function and its estimates are:
\[\begin{split} \log_{10}(\mathrm{pre\_art\_bmi}) = \beta_0 &+ \beta_\mathrm{age} \cdot \mathrm{age} + \beta_\mathrm{age\_1} \cdot \mathrm{age\_1} + \beta_\mathrm{age\_2} \cdot \mathrm{age\_2}+ \beta_\mathrm{art\_init\_year} \cdot \mathrm{art\_init\_year}\\[2ex] &+ \beta_\mathrm{art\_init\_year\_1} \cdot \mathrm{art\_init\_year\_1} + \beta_\mathrm{art\_init\_year\_2} \cdot \mathrm{art\_init\_year\_2} \end{split}\]Table 26: Pre-ART BMI Model 4 Estimates

Post-ART BMI
Post-ART BMI (\(\mathrm{post\_art\_bmi}\)) is calculated using only a single model for all 15 subpopulations. We model \(\mathrm{sqrt\_post\_art\_bmi}\) as a function of \(\mathrm{age}\), square root of pre-ART BMI (\(\mathrm{sqrt\_pre\_art\_bmi}\)), square root of CD4 count at ART initiation (\(\mathrm{sqrt\_init\_cd4}\)), and square root of CD4 count 2 years after ART initiation (\(\mathrm{sqrt\_cd4\_post\_art}\)) modeled by restricted cubic splines as well as a linear function of \(\mathrm{art\_init\_year}\). The full equation is:
\[\begin{split} \mathrm{sqrt\_post\_art\_bmi} = \beta_0 &+ \beta_\mathrm{age} \cdot \mathrm{age} + \beta_\mathrm{age\_1} \cdot \mathrm{age\_1} + \beta_\mathrm{age\_2} \cdot \mathrm{age\_2} + \beta_\mathrm{sqrt\_pre\_art\_bmi} \cdot \mathrm{sqrt\_pre\_art\_bmi}\\[2ex] &+ \beta_\mathrm{sqrt\_pre\_art\_bmi\_1} \cdot \mathrm{sqrt\_pre\_art\_bmi\_1}+ \beta_\mathrm{sqrt\_pre\_art\_bmi\_2} \cdot \mathrm{sqrt\_pre\_art\_bmi\_2}\\[2ex] &+ \beta_\mathrm{sqrt\_init\_cd4} \cdot \mathrm{sqrt\_init\_cd4} + \beta_\mathrm{sqrt\_init\_cd4\_1} \cdot \mathrm{sqrt\_init\_cd4\_1} + \beta_\mathrm{sqrt\_init\_cd4\_2} \cdot \mathrm{sqrt\_init\_cd4\_2}\\[2ex] &+ \beta_\mathrm{sqrt\_cd4\_post\_art} \cdot \mathrm{sqrt\_cd4\_post\_art} + \beta_\mathrm{sqrt\_cd4\_post\_art\_1} \cdot \mathrm{sqrt\_cd4\_post\_art\_1}\\[2ex] &+ \beta_\mathrm{sqrt\_cd4\_post\_art\_2} \cdot \mathrm{sqrt\_cd4\_post\_art\_2} + \beta_\mathrm{art\_init\_year} \cdot \mathrm{art\_init\_year} \end{split}\]The various knot locations are in the following tables.
Table 27: Post-ART BMI Age Knots
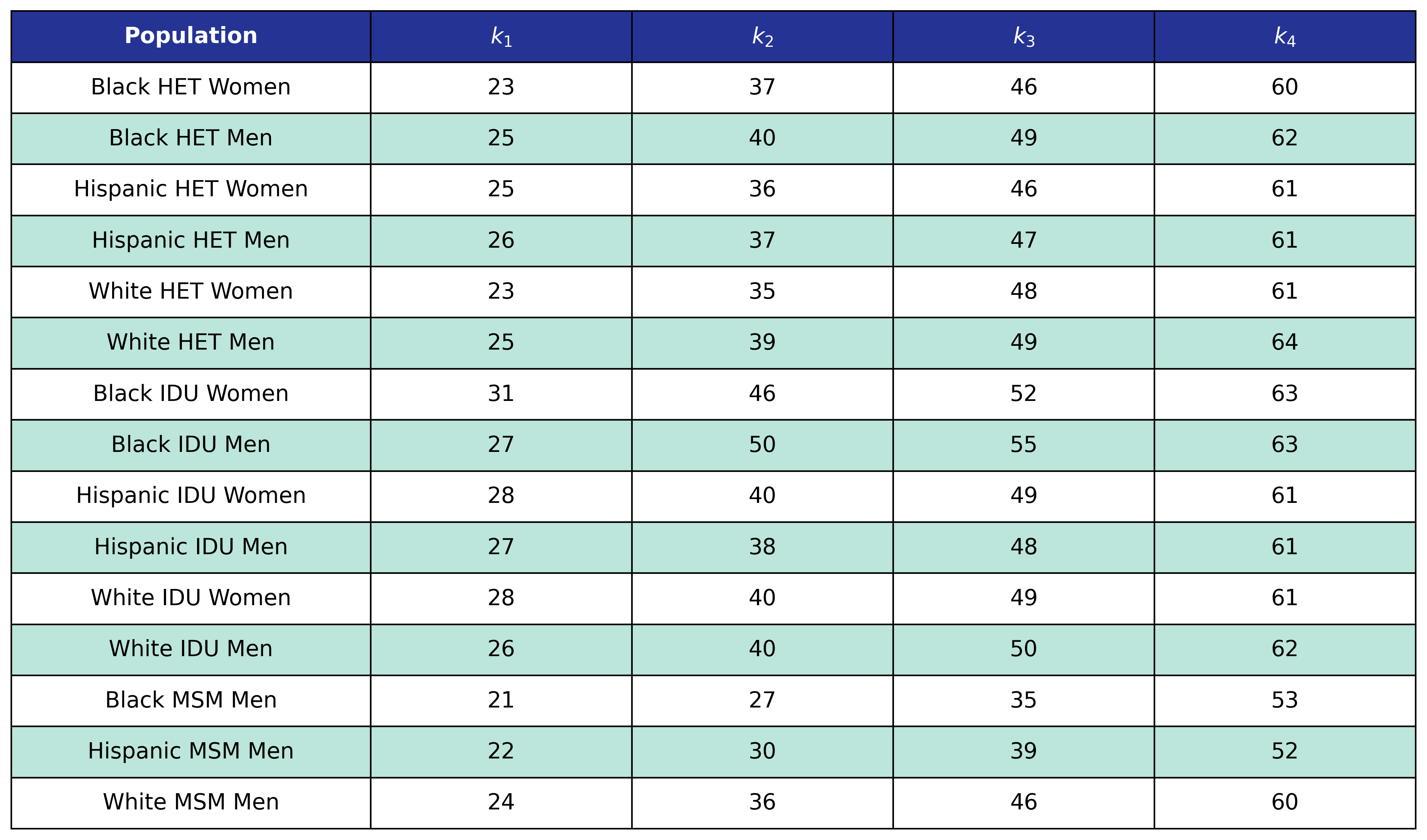
Table 28: Post-ART BMI Pre-ART CD4 Knots
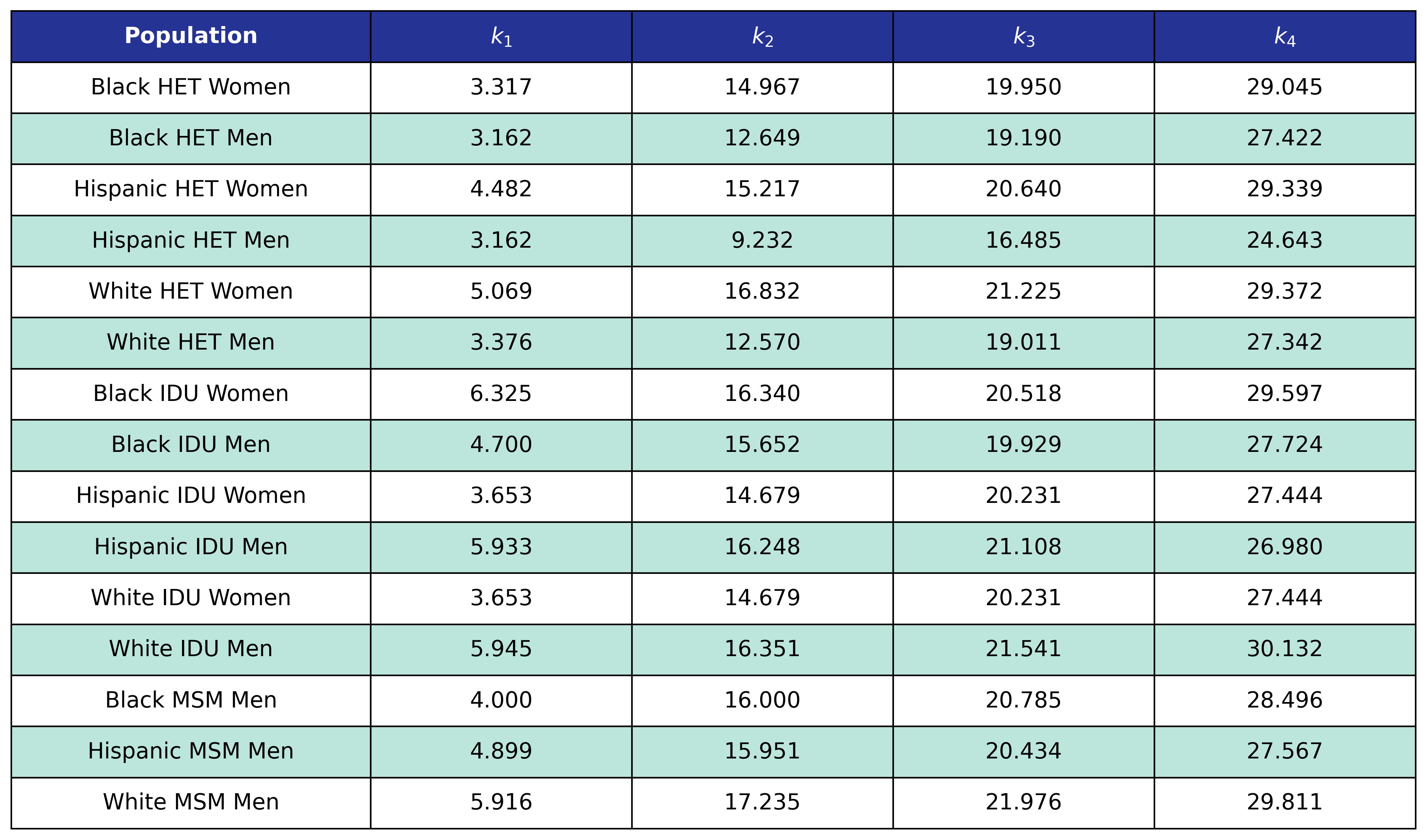
Table 28: Post-ART BMI Post-ART CD4 Knots
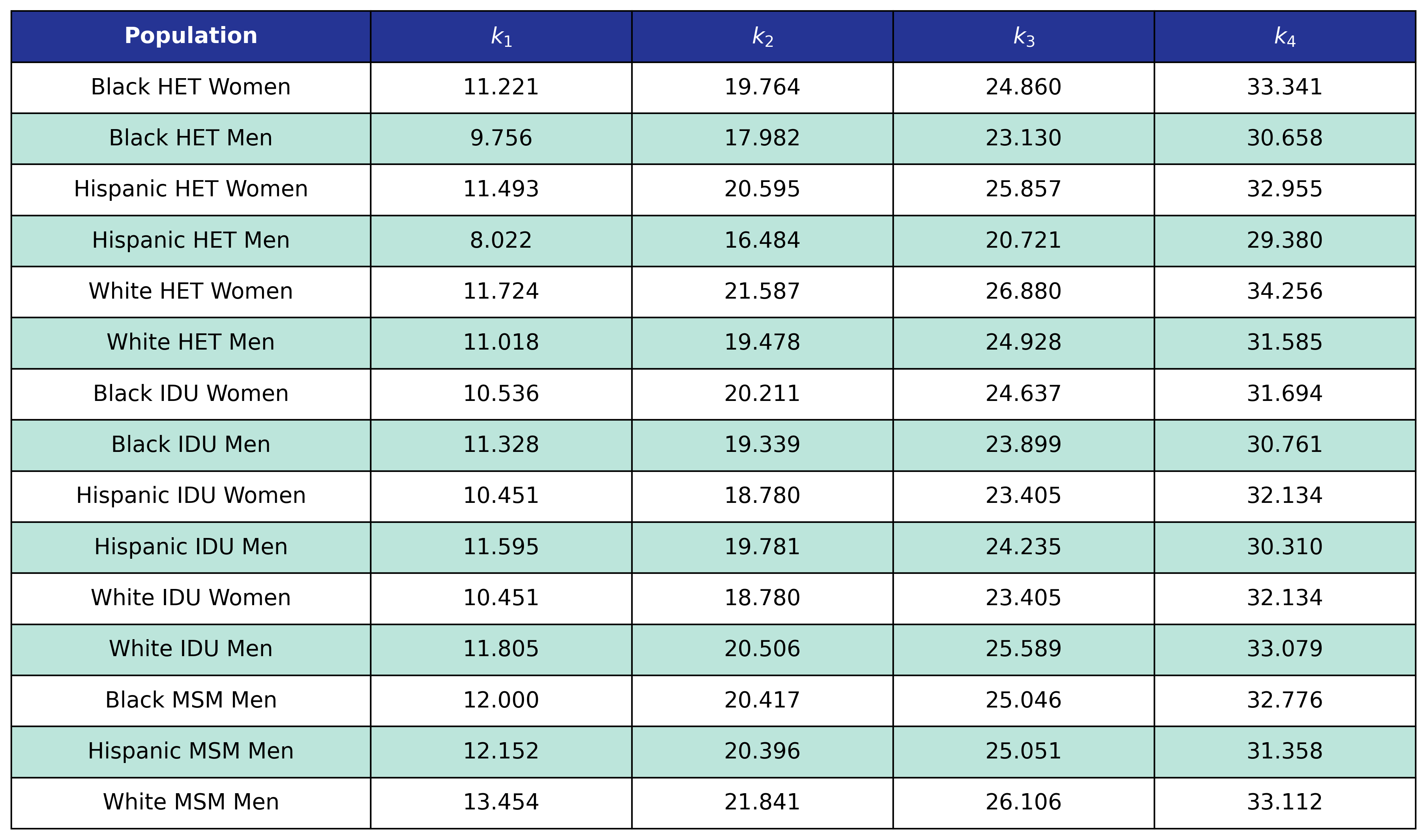
The estimates are as follows:
Table 29: Post-ART BMI Coefficient Estimates
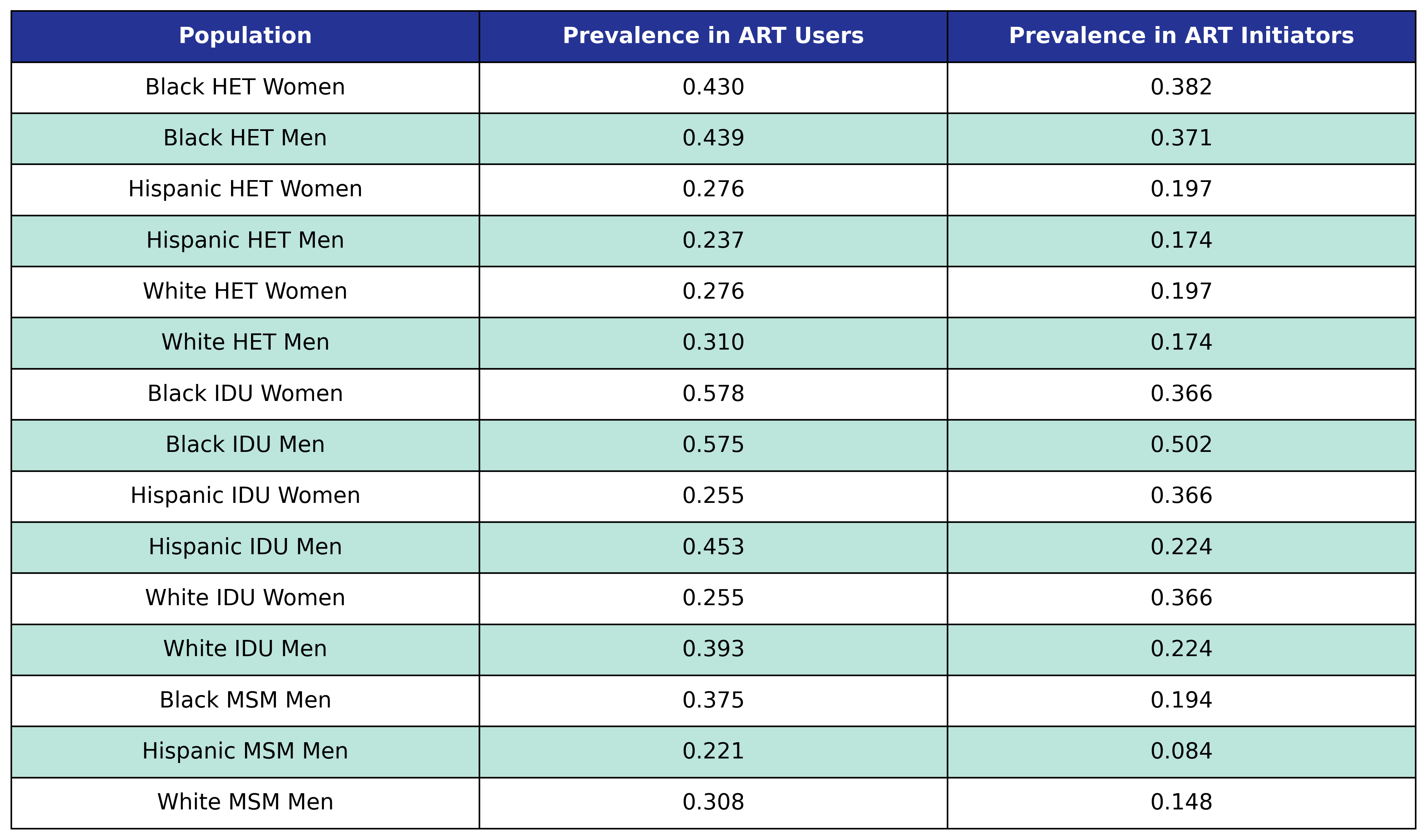
Risk Factors
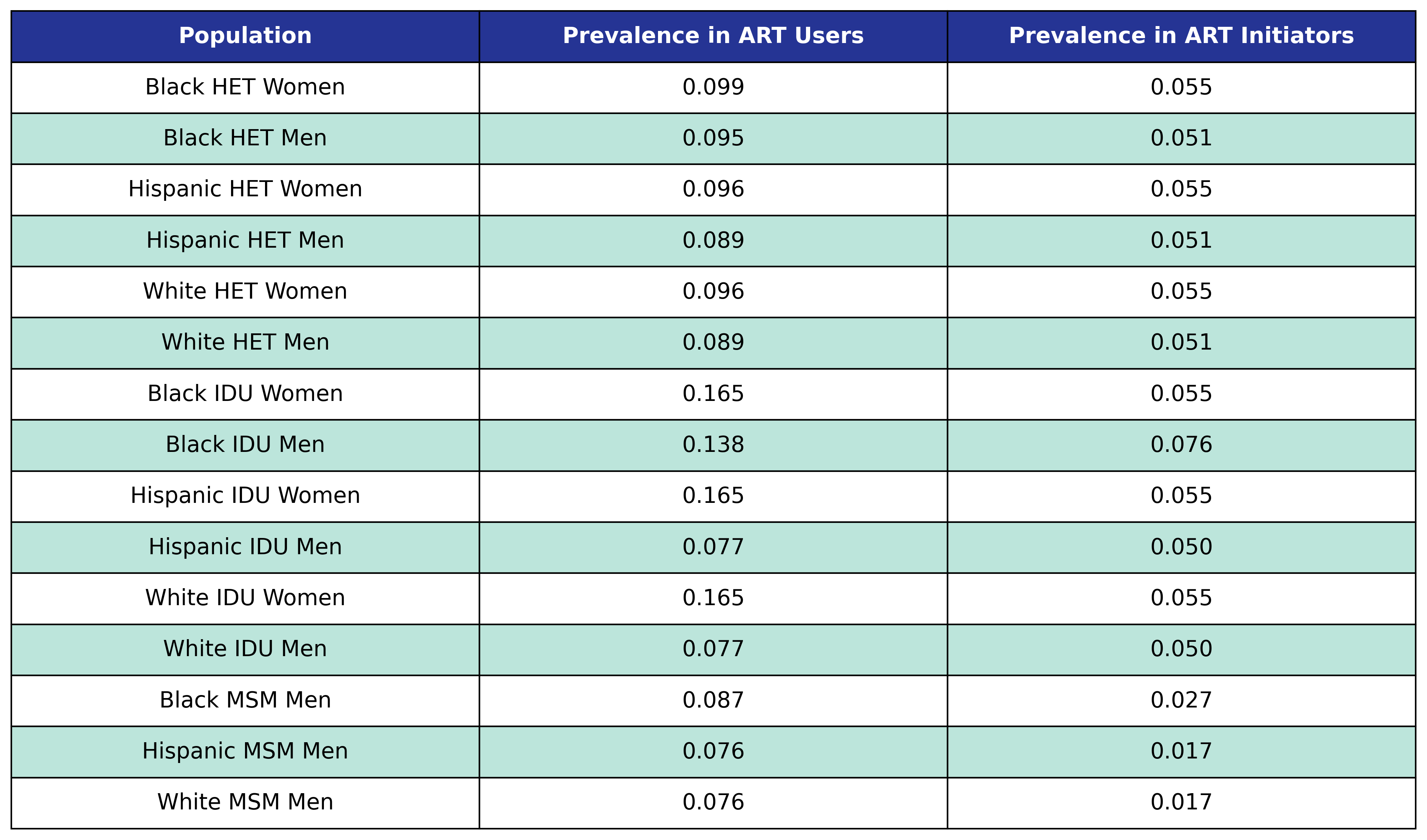
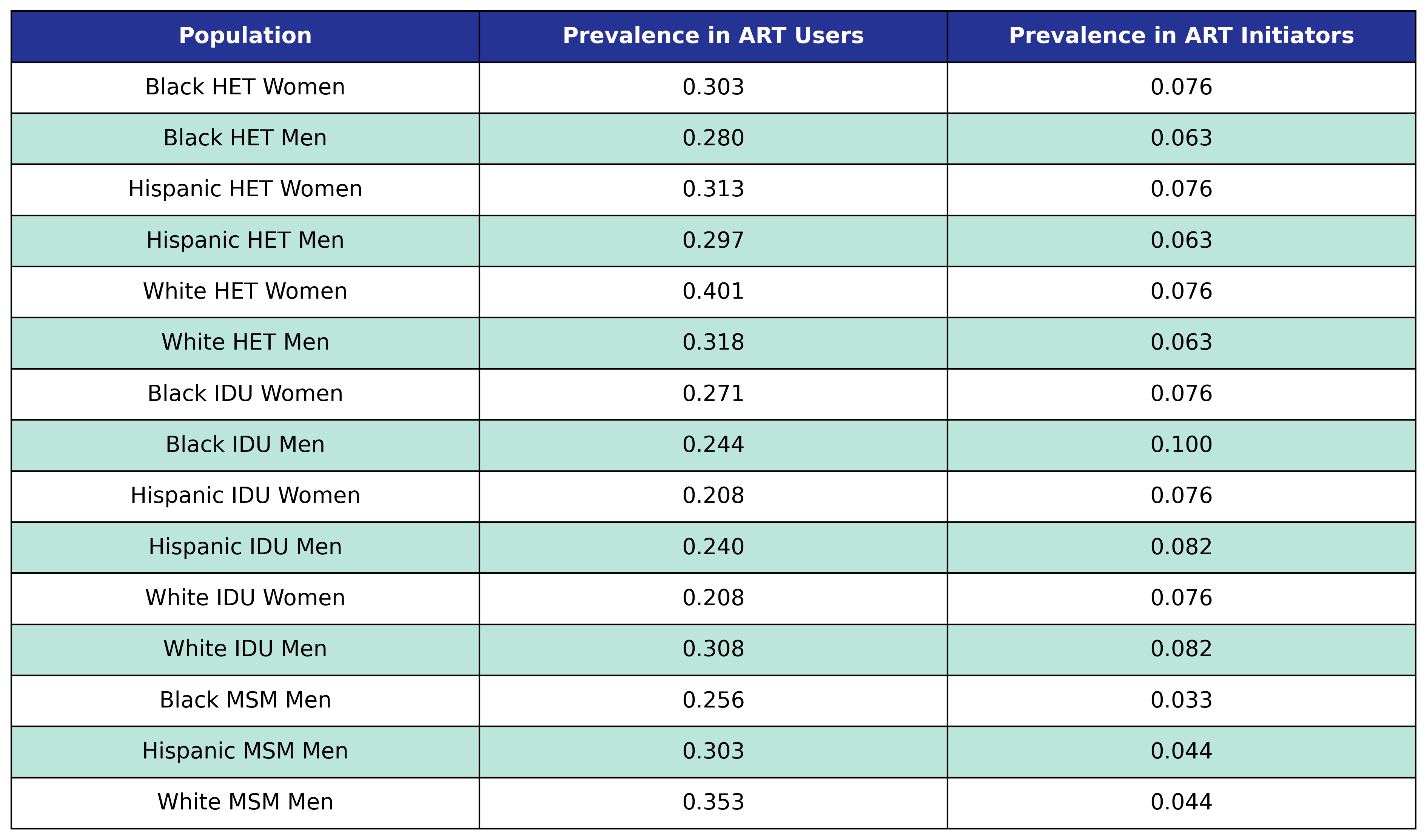
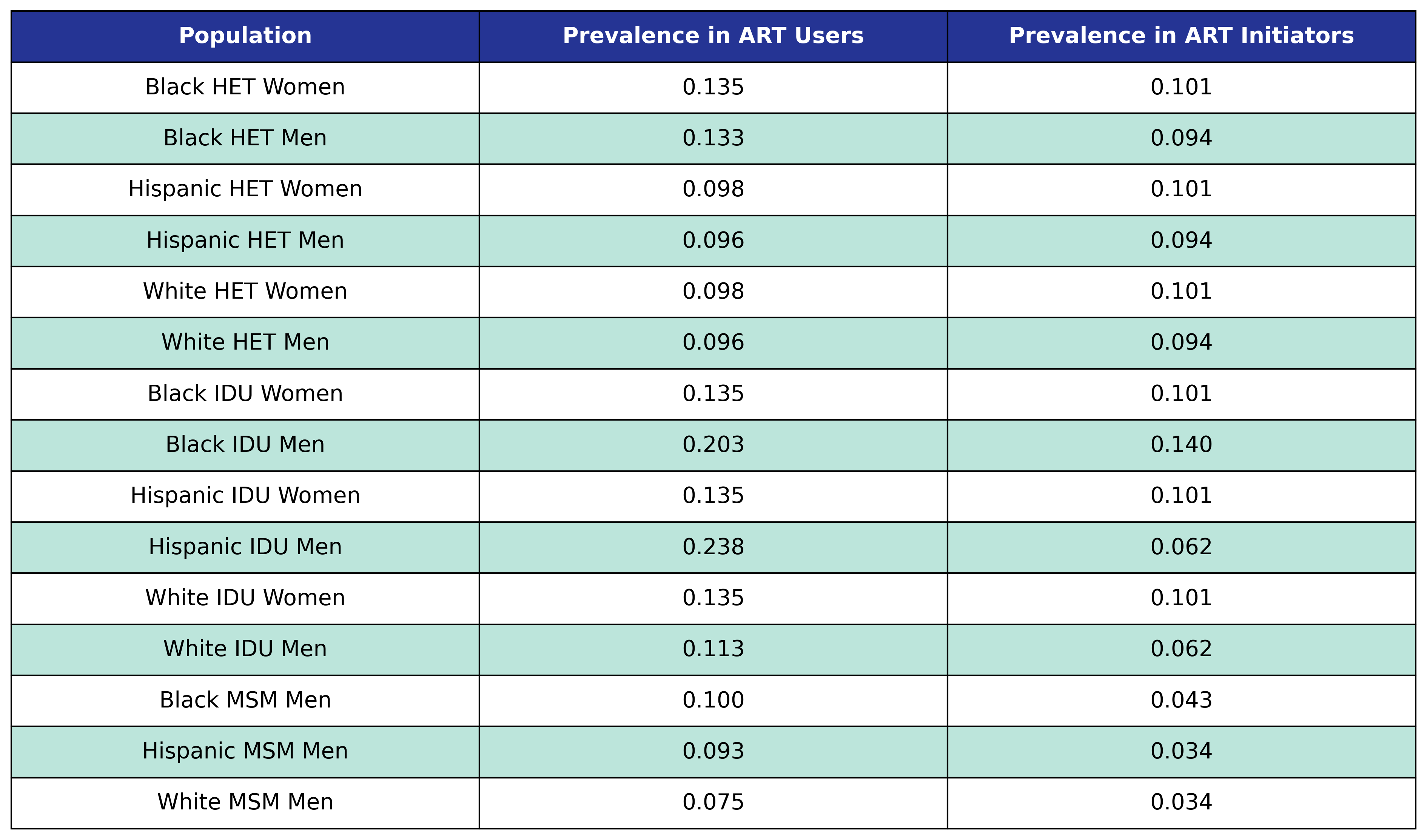
The stage 0 conditions are smoking and hepatitis C (HCV). These conditions are assumed to be ever/never for each person in the population, meaning that no incidence is modeled. From NA-ACCORD data, we generate an average prevalence in ART users from 2009 - 2017 for our initial 2009 population and an average prevalence in ART initiators from 2009 - 2017 for our initiator population.
Smoking
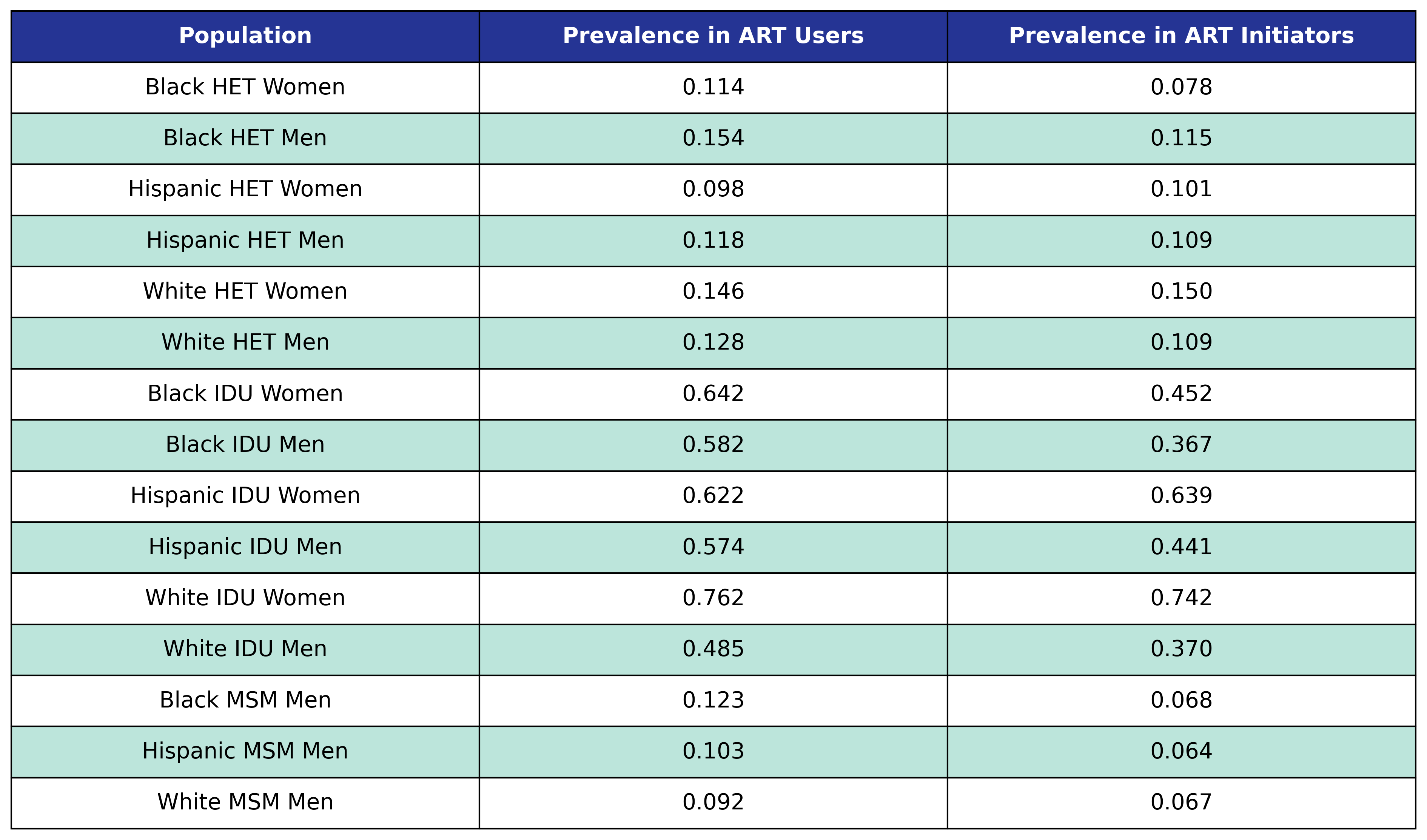
At population creation, each agent has a probability of being a smoker given by the following table:
Table 30: Smoking Prevalences
Hepatitis C Virus
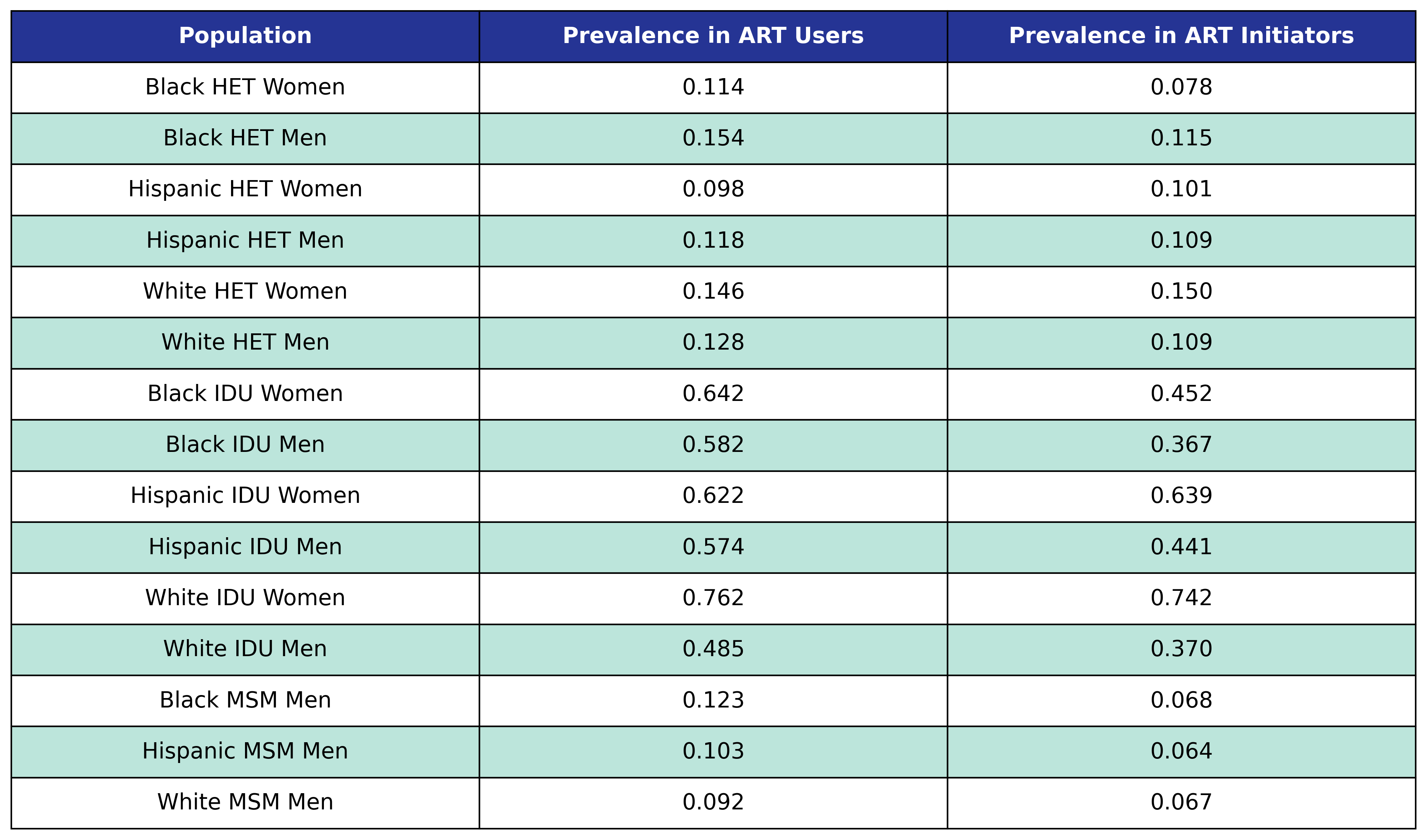
At population creation, each agent has a probability of ever having hepatitis C virus given by the following table:
Table 31: Hepatitis C Prevalence
Stage 1
The stage 1 conditions are anxiety and depression. Prevalence in the ART user and initiator populations is computed in a similar way to the stage 0 conditions. However, only the 2009 NA-ACCORD population was used to model ART users in 2009. Prevalence in ART initiators was taken 2009 - 2017. In addition, we allow for incidence of both conditions in addition to prevalence. Incidence is modeled using logistic regression.
Anxiety
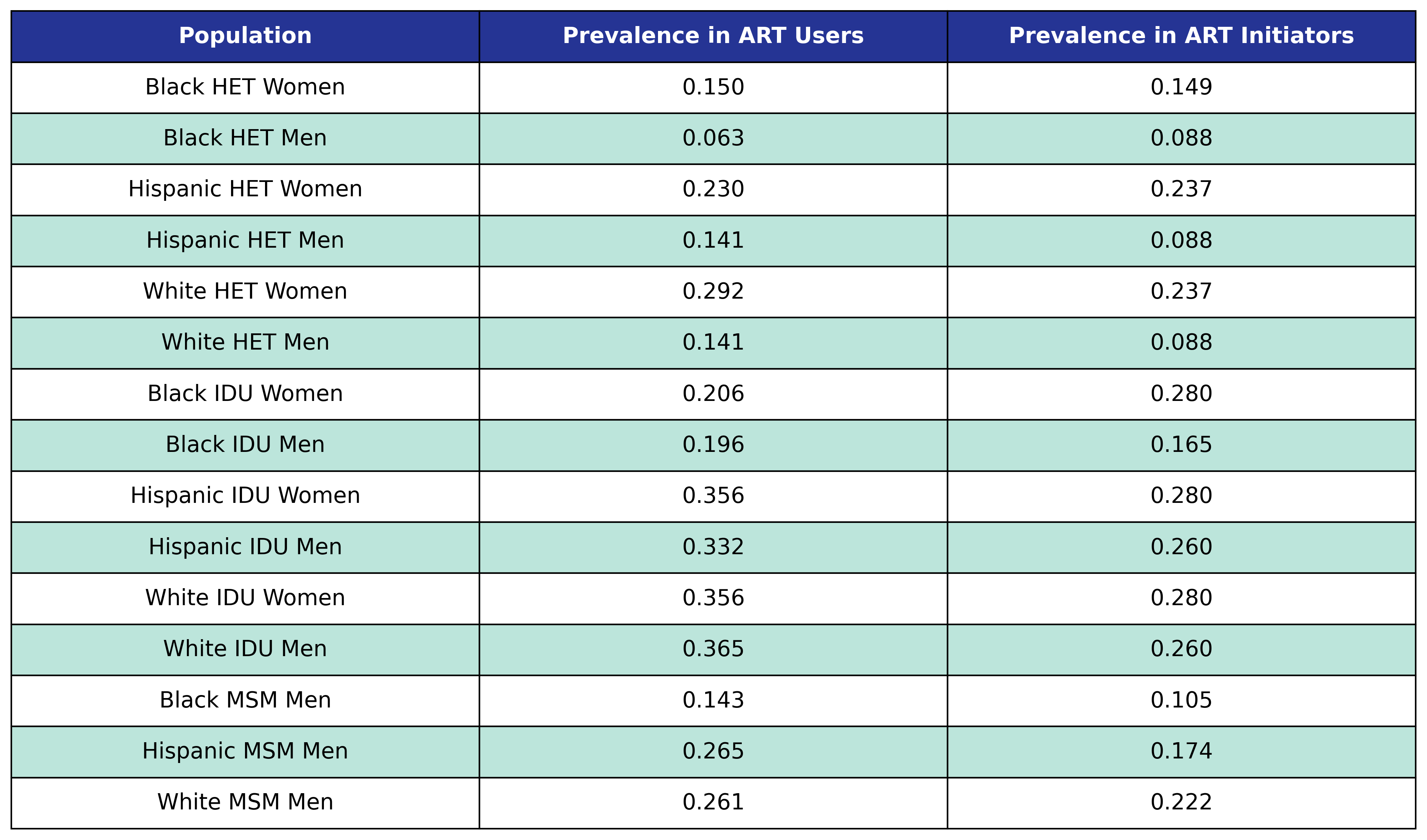
The prevalence of anxiety in ART users and initiators is shown in the following table:
Table 32: Anxiety Prevalence
We use logistic regression to model the probability of incidence of anxiety as a function of calendar year (\(\mathrm{year}\)), age (\(\mathrm{age}\)), square root of CD4 count at ART initiation (\(\mathrm{sqrt\_init\_cd4}\)), number of years since ART initiation (\(\mathrm{time\_since\_art}\)), smoking status (\(\mathrm{smoking}\)), HCV status (\(\mathrm{hcv}\)) and depression status (\(\mathrm{depression}\)). The status variables are encoded as Boolean variables. This choice of regressors leads to the following regression equation:
\[\begin{split} \mathrm{logit}(p) = \beta_0 &+ \beta_\mathrm{year} \cdot\mathrm{year} + \beta_\mathrm{age} \cdot \mathrm{age} + \beta_\mathrm{sqrt\_init\_cd4}\cdot\mathrm{sqrt\_init\_cd4} + \beta_\mathrm{time\_since\_art} \cdot \mathrm{time\_since\_art} \\[2ex] &+ \beta_\mathrm{smoking} \cdot \mathrm{smoking} + \beta_\mathrm{hcv} \cdot \mathrm{hcv} + \beta_\mathrm{depression} \cdot \mathrm{depression} \end{split}\]where
\[\mathrm{logit}(p) = \log \frac{p}{1 - p}\]is the logit function and \(p\) is the probability of incidence of anxiety.
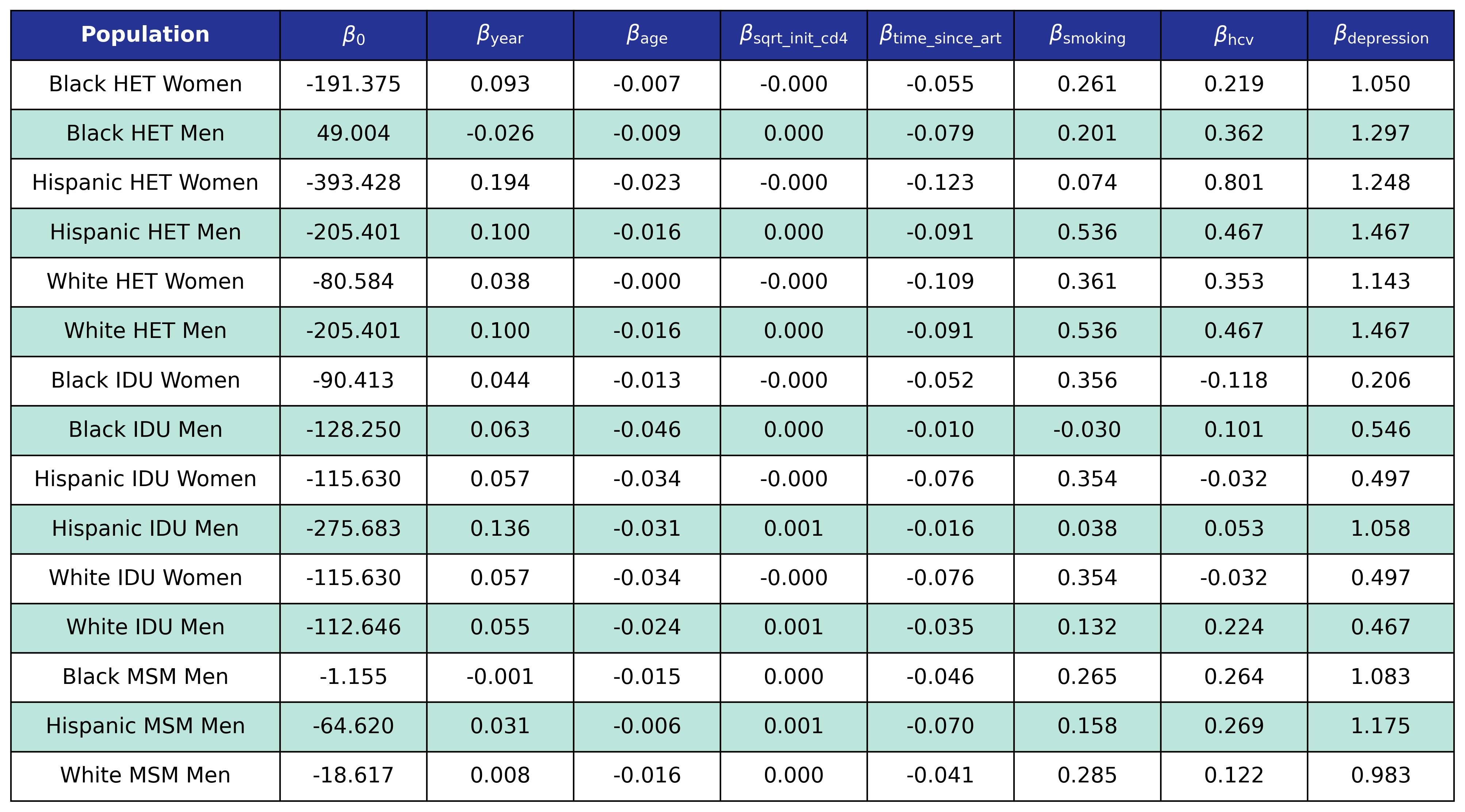
The fitted coefficients are:
Table 33: Anxiety Incidence
Depression
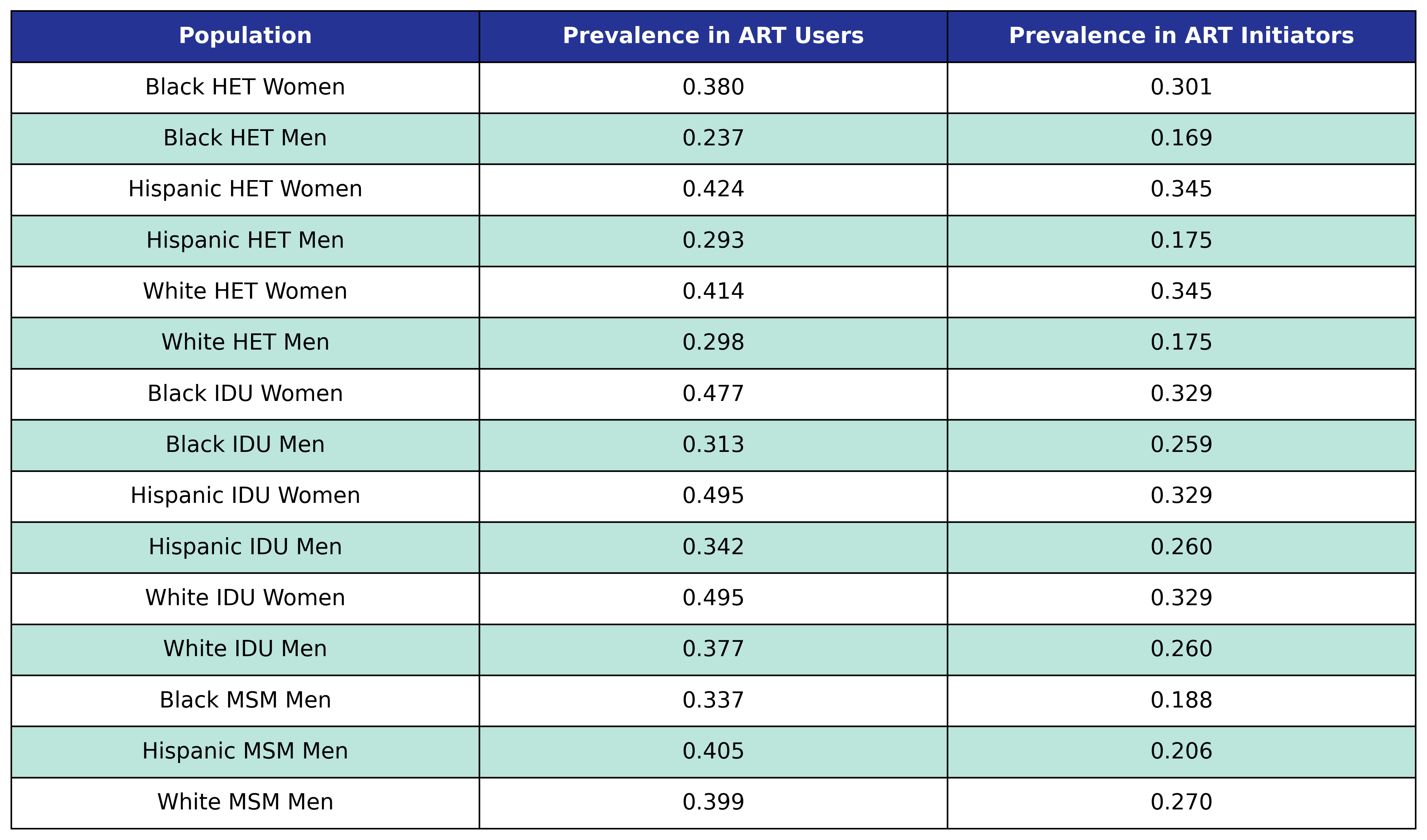
The prevalence of depression in ART users and initiators is shown in the following table:
Table 34: Depression Prevalence
We use logistic regression to model the probability of incidence of depression as a function of calendar year (\(\mathrm{year}\)), age (\(\mathrm{age}\)), square root of CD4 count at ART initiation (\(\mathrm{sqrt\_init\_cd4}\)), number of years since ART initiation (\(\mathrm{time\_since\_art}\)), smoking status (\(\mathrm{smoking}\)), HCV status (\(\mathrm{hcv}\)) and anxiety status (\(\mathrm{anxiety}\)). The status variables are encoded as Boolean variables. This choice of regressors leads to the following regression equation:
\[\begin{split} \mathrm{logit}(p) = \beta_0 &+ \beta_\mathrm{year} \cdot\mathrm{year} + \beta_\mathrm{age} \cdot \mathrm{age} + \beta_\mathrm{sqrt\_init\_cd4}\cdot\mathrm{sqrt\_init\_cd4} + \beta_\mathrm{time\_since\_art} \cdot \mathrm{time\_since\_art} \\[2ex] &+ \beta_\mathrm{smoking} \cdot \mathrm{smoking} + \beta_\mathrm{hcv} \cdot \mathrm{hcv} + \beta_\mathrm{anxiety} \cdot \mathrm{anxiety} \end{split}\]where
\[\mathrm{logit}(p) = \log \frac{p}{1 - p}\]is the logit function and \(p\) is the probability of incidence of depression.
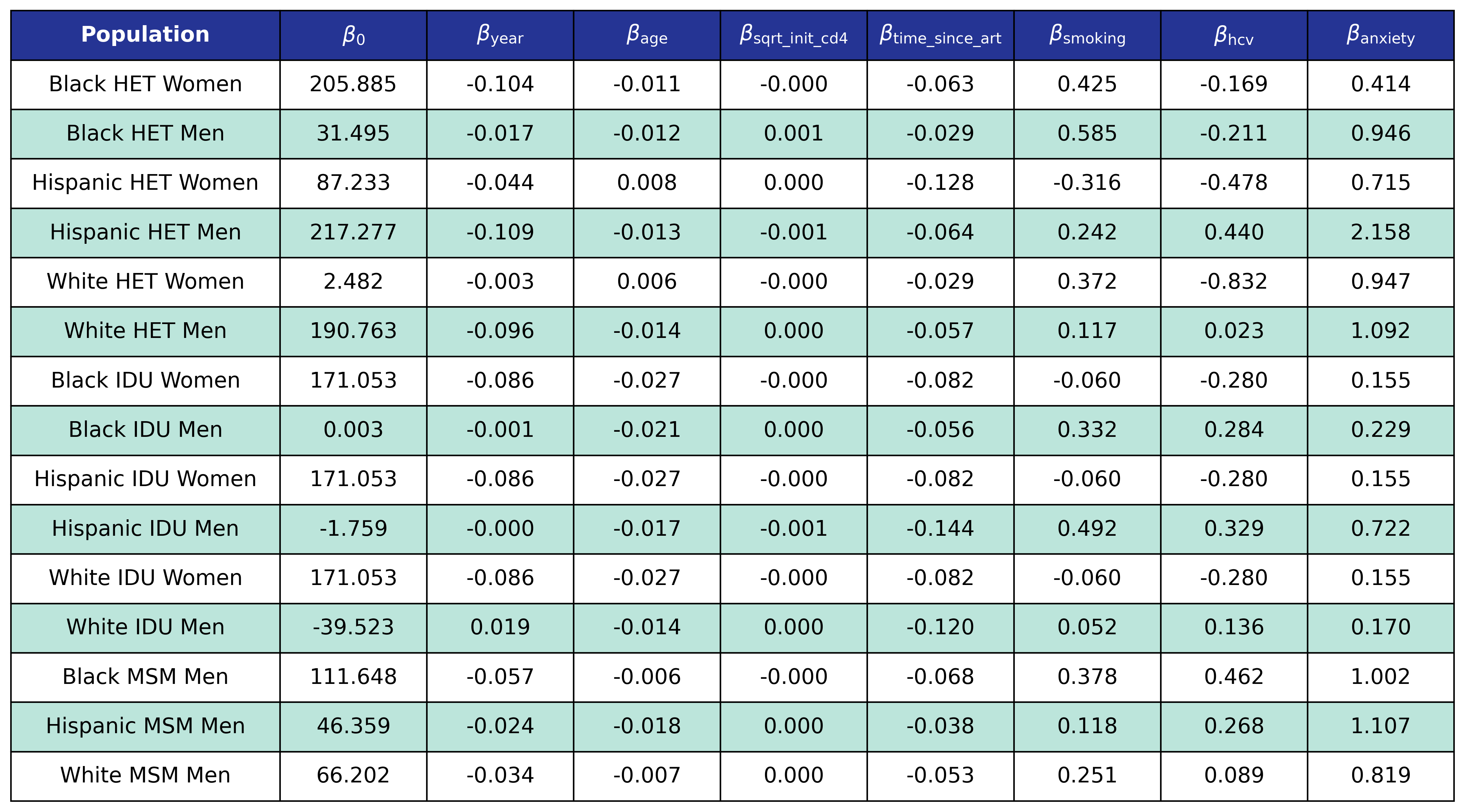
The fitted coefficients are:
Table 35: Depression Incidence
Stage 2
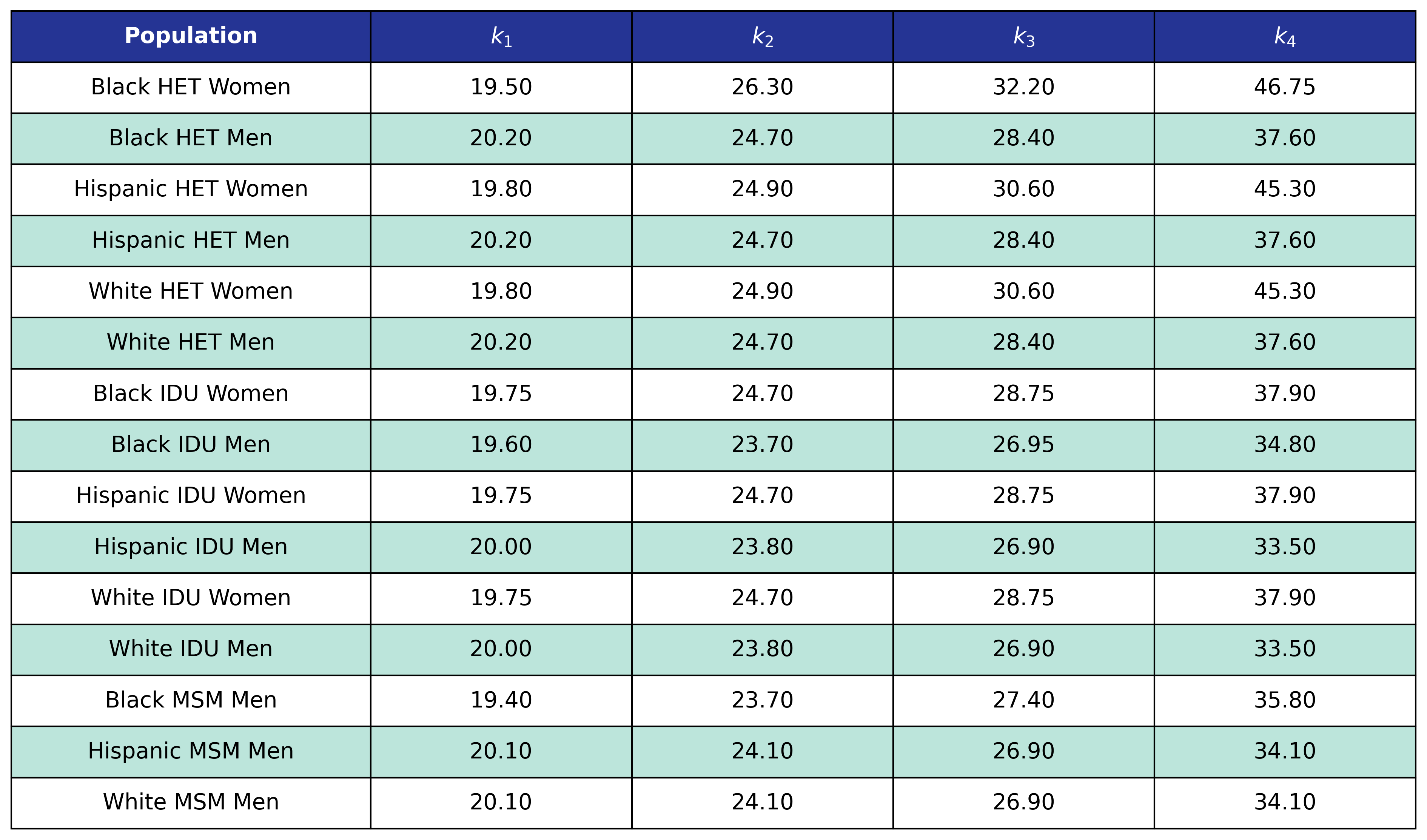
The stage 2 conditions are chronic kidney disease (CKD), hyperlipidemia, diabetes mellitus, and hypertension. Prevalence in the 2009 ART user population is taken from the 2009 NA-ACCORD population, while prevalence in ART initiators was taken from the 2009 - 2017 NA-ACCORD ART initiator population. Incidence is modeled using logistic regression and is based on NA-ACCORD data. The logistic regression models the logit of probability for incidence of a stage 2 condition as a linear function of calendar year (\(\mathrm{year}\)), age (\(\mathrm{age}\)), square root of CD4 count at ART initiation (\(\mathrm{sqrt\_init\_cd4}\)), number of years since ART initiation (\(\mathrm{time\_since\_art}\)), change in BMI after ART initiation (\(\mathrm{delta\_bmi}\)) and BMI after ART initiation (\(\mathrm{post\_art\_bmi}\)) modeled as restricted cubic splines, stage 0 condition status (\(\mathrm{smoking}\), \(\mathrm{hcv}\)), stage 1 condition status (\(\mathrm{anxiety}\), \(\mathrm{depression}\)), and other stage 2 condition status (\(\mathrm{ckd}\), \(\mathrm{lipid}\), \(\mathrm{diabetes}\), \(\mathrm{hypertension}\)).
Chronic Kidney Disease
At the beginning of the simulation each member of the initial population begins with \(\mathrm{ckd} = 1\) with probability given by the first column in the table. At the start of each year new ART initiators are added where \(\mathrm{ckd} = 1\) with probability given by the second column in the table.
Table 36: CKD Prevalence
At the beginning of each year the in care and out of care populations with \(\mathrm{ckd} = 0\) have probability for incidence of CKD given by
\[\begin{split} \mathrm{logit}(p) = \beta_0 &+ \beta_\mathrm{year}\cdot\mathrm{year} + \beta_\mathrm{age}\cdot\mathrm{age} + \beta_\mathrm{sqrt\_init\_cd4}\cdot\mathrm{sqrt\_init\_cd4} + \beta_\mathrm{time\_since\_art} \cdot \mathrm{time\_since\_art} \\[2ex] &+ \beta_\mathrm{delta\_bmi} \cdot \mathrm{delta\_bmi} + \beta_\mathrm{delta\_bmi\_1} \cdot \mathrm{delta\_bmi\_1} + \beta_\mathrm{delta\_bmi\_2} \cdot \mathrm{delta\_bmi\_2}\\[2ex] &+ \beta_\mathrm{post\_art\_bmi} \cdot \mathrm{post\_art\_bmi} + \beta_\mathrm{post\_art\_bmi\_1} \cdot \mathrm{post\_art\_bmi\_1} + \beta_\mathrm{post\_art\_bmi\_2} \cdot \mathrm{post\_art\_bmi\_2}\\[2ex] &+ \beta_\mathrm{smoking} \cdot \mathrm{smoking} + \beta_\mathrm{hcv} \cdot \mathrm{hcv} + \beta_\mathrm{anxiety} \cdot \mathrm{anxiety} + \beta_\mathrm{depression} \cdot \mathrm{depression}\\[2ex] &+ \beta_\mathrm{lipid} \cdot \mathrm{lipid} + \beta_\mathrm{diabetes} \cdot \mathrm{diabetes} + \beta_\mathrm{hypertension} \cdot \mathrm{hypertension} \end{split}\]where
\[\mathrm{logit}(p) = \log \frac{p}{1 - p}\]is the logit function and \(p\) is the probability of incidence of CKD.
The fitted coefficients and knot locations are given in the following tables.
Table 37: CKD Incidence
Table 38: CKD Delta BMI Knots
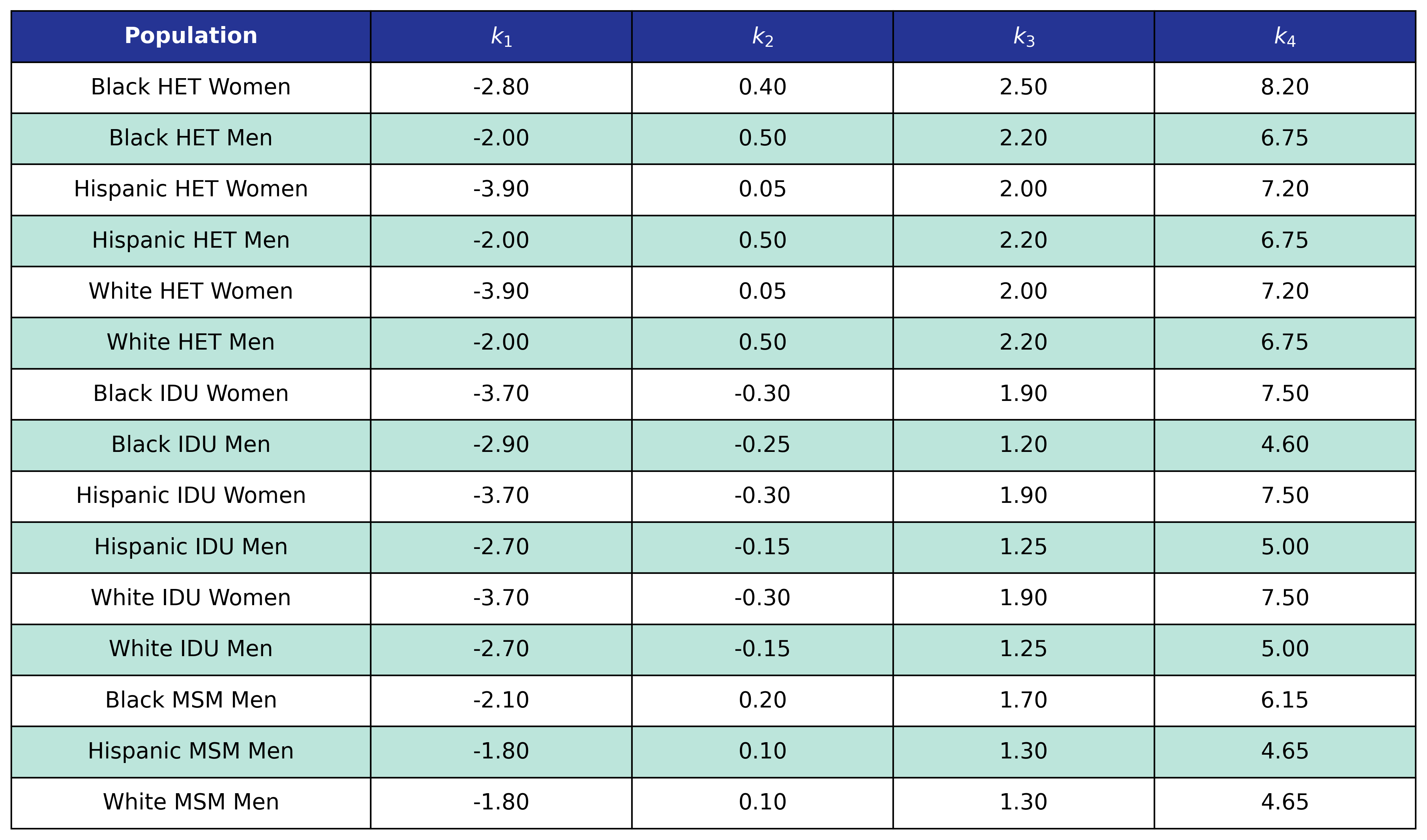
Table 39: CKD Post-ART BMI Knots
Hyperlipidemia
At the beginning of the simulation each member of the initial population begins with \(\mathrm{lipid} = 1\) with probability given by the first column in the table. At the start of each year new ART initiators are added where \(\mathrm{lipid} = 1\) with probability given by the second column in the table.
Table 40: Hyperlipidemia Prevalence
At the beginning of each year the in care and out of care populations with \(\mathrm{lipid} = 0\) have probability for incidence of hyperlipidemia given by
\[\begin{split} \mathrm{logit}(p) = \beta_0 &+ \beta_\mathrm{year}\cdot\mathrm{year} + \beta_\mathrm{age}\cdot\mathrm{age} + \beta_\mathrm{sqrt\_init\_cd4}\cdot\mathrm{sqrt\_init\_cd4} + \beta_\mathrm{time\_since\_art} \cdot \mathrm{time\_since\_art} \\[2ex] &+ \beta_\mathrm{delta\_bmi} \cdot \mathrm{delta\_bmi} + \beta_\mathrm{delta\_bmi\_1} \cdot \mathrm{delta\_bmi\_1} + \beta_\mathrm{delta\_bmi\_2} \cdot \mathrm{delta\_bmi\_2}\\[2ex] &+ \beta_\mathrm{post\_art\_bmi} \cdot \mathrm{post\_art\_bmi} + \beta_\mathrm{post\_art\_bmi\_1} \cdot \mathrm{post\_art\_bmi\_1} + \beta_\mathrm{post\_art\_bmi\_2} \cdot \mathrm{post\_art\_bmi\_2} \\[2ex] &+ \beta_\mathrm{smoking} \cdot \mathrm{smoking} + \beta_\mathrm{hcv} \cdot \mathrm{hcv} + \beta_\mathrm{anxiety} \cdot \mathrm{anxiety} + \beta_\mathrm{depression} \cdot \mathrm{depression} \\[2ex] &+ \beta_\mathrm{ckd} \cdot \mathrm{ckd} + \beta_\mathrm{diabetes} \cdot \mathrm{diabetes} + \beta_\mathrm{hypertension} \cdot \mathrm{hypertension} \end{split}\]where
\[\mathrm{logit}(p) = \log \frac{p}{1 - p}\]is the logit function and \(p\) is the probability of incidence of hyperlipidemia.
The fitted coefficients and knot locations are given in the following tables.
Table 41: Hyperlipidemia Incidence
Table 42: Hyperlipidemia Delta BMI Knots
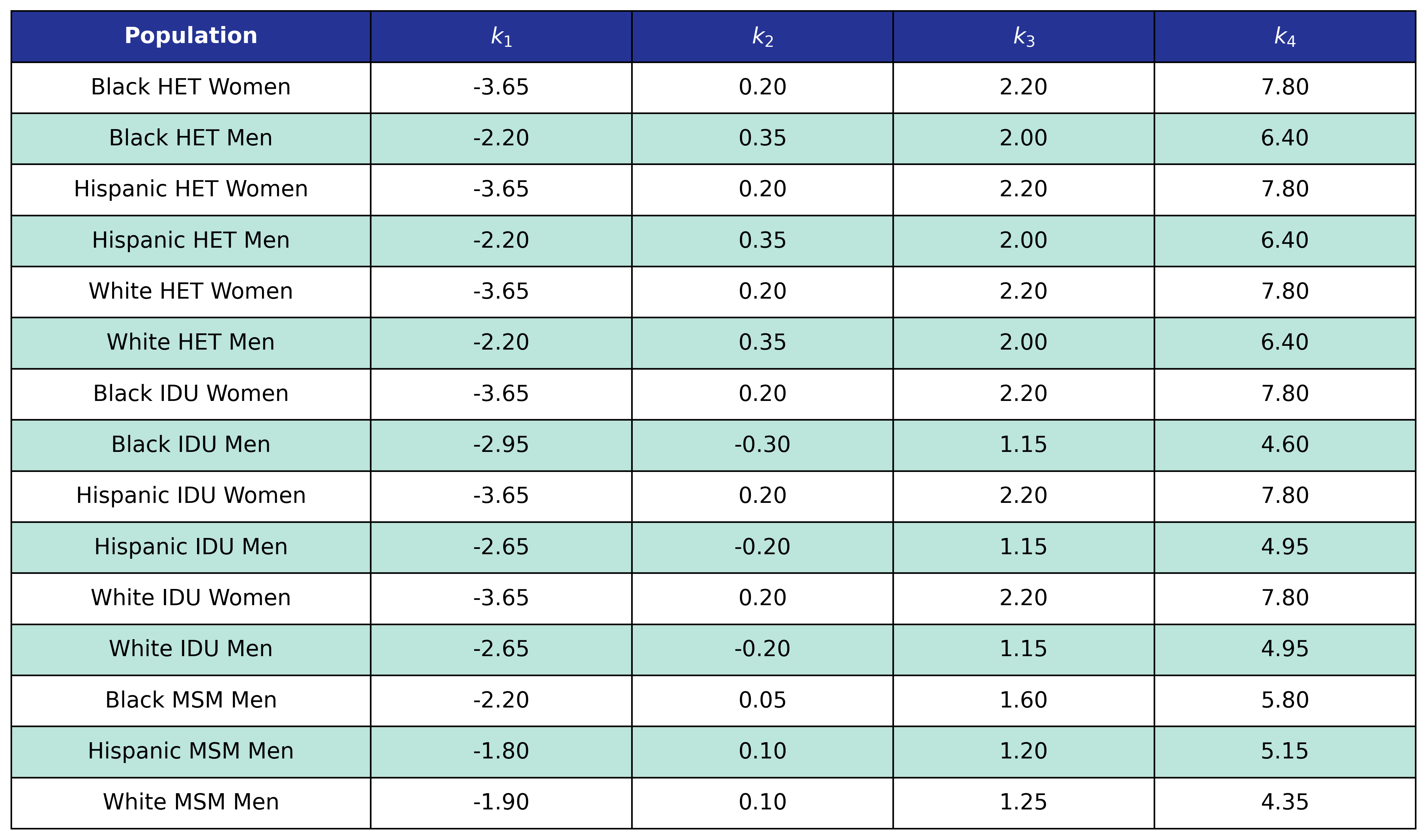
Table 43: Hyperlipidemia Post-ART BMI Knots
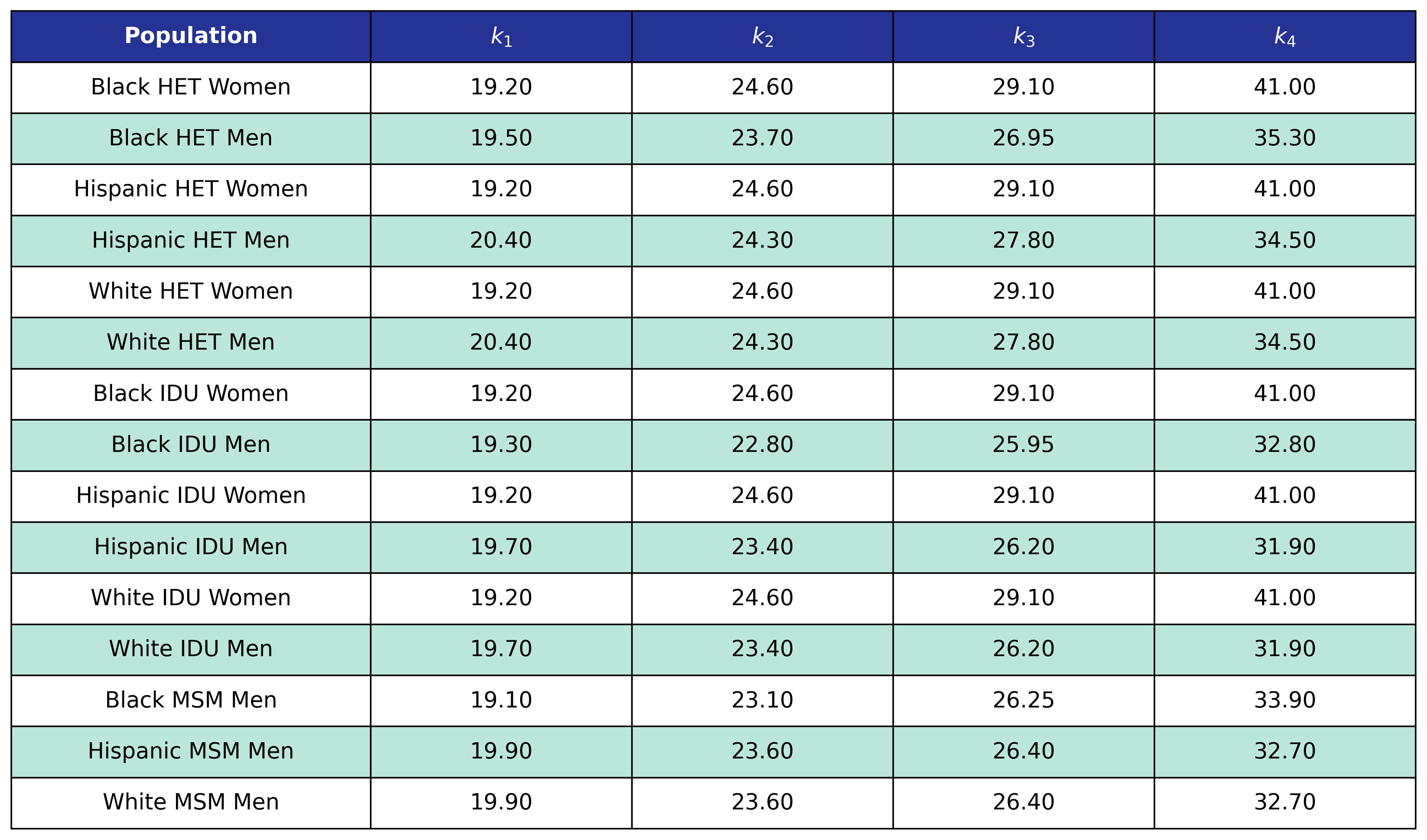
Diabetes Mellitus
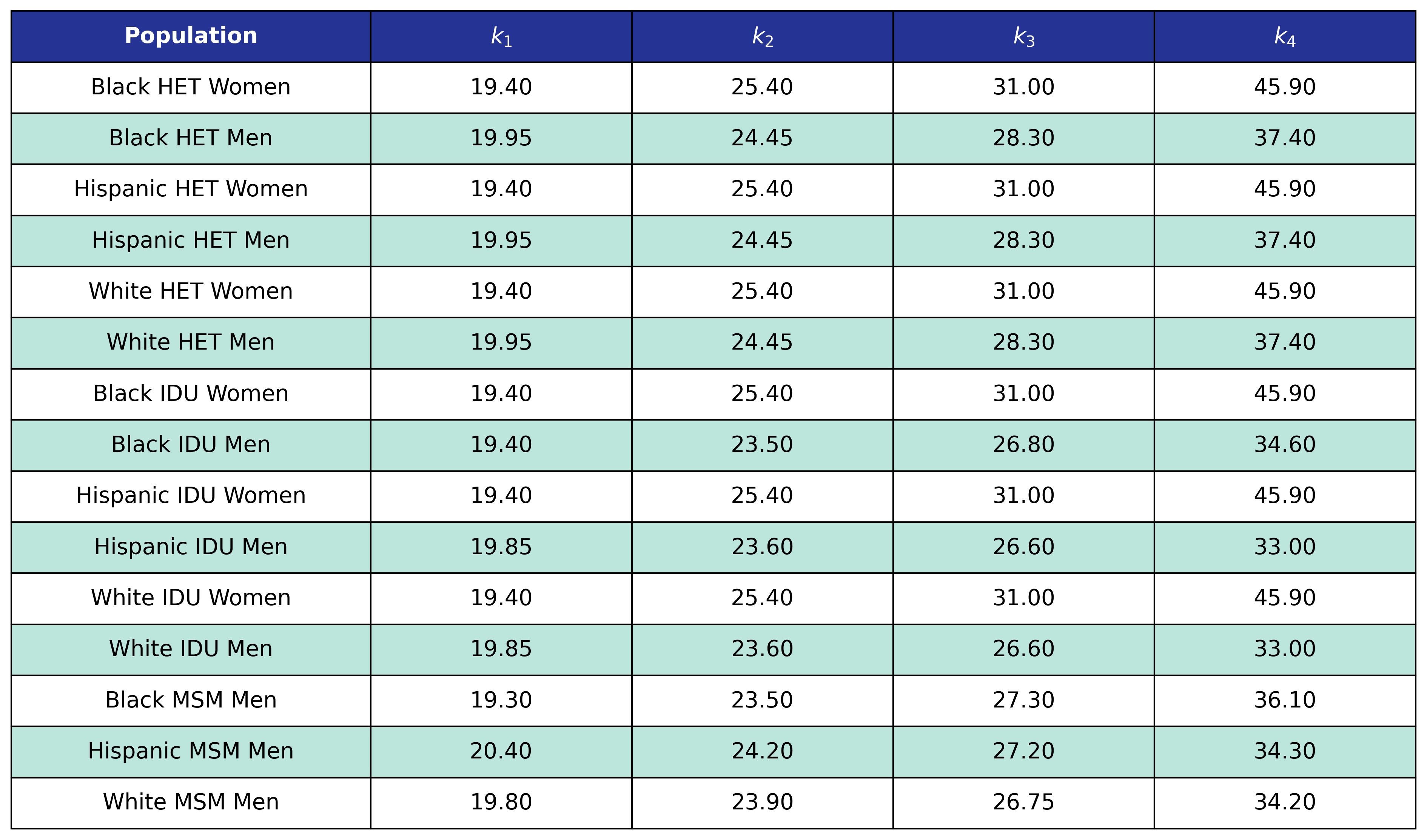
At the beginning of the simulation each member of the initial population begins with \(\mathrm{diabetes} = 1\) with probability given by the first column in the table. At the start of each year new ART initiators are added where \(\mathrm{diabetes} = 1\) with probability given by the second column in the table.
Table 44: Diabetes Prevalence
At the beginning of each year the in care and out of care populations with \(\mathrm{diabetes} = 0\) have probability for incidence of diabetes mellitus given by
\[\begin{split} \mathrm{logit}(p) = \beta_0 &+ \beta_\mathrm{year}\cdot\mathrm{year} + \beta_\mathrm{age}\cdot\mathrm{age} + \beta_\mathrm{sqrt\_init\_cd4}\cdot\mathrm{sqrt\_init\_cd4} + \beta_\mathrm{time\_since\_art} \cdot \mathrm{time\_since\_art} \\[2ex] &+ \beta_\mathrm{delta\_bmi} \cdot \mathrm{delta\_bmi} + \beta_\mathrm{delta\_bmi\_1} \cdot \mathrm{delta\_bmi\_1} + \beta_\mathrm{delta\_bmi\_2} \cdot \mathrm{delta\_bmi\_2} \\[2ex] &+ \beta_\mathrm{post\_art\_bmi} \cdot \mathrm{post\_art\_bmi} + \beta_\mathrm{post\_art\_bmi\_1} \cdot \mathrm{post\_art\_bmi\_1} + \beta_\mathrm{post\_art\_bmi\_2} \cdot \mathrm{post\_art\_bmi\_2} \\[2ex] &+ \beta_\mathrm{smoking} \cdot \mathrm{smoking} + \beta_\mathrm{hcv} \cdot \mathrm{hcv} + \beta_\mathrm{anxiety} \cdot \mathrm{anxiety} + \beta_\mathrm{depression} \cdot \mathrm{depression} \\[2ex] &+ \beta_\mathrm{ckd} \cdot \mathrm{ckd} + \beta_\mathrm{lipid} \cdot \mathrm{lipid} + \beta_\mathrm{hypertension} \cdot \mathrm{hypertension} \end{split}\]where
\[\mathrm{logit}(p) = \log \frac{p}{1 - p}\]is the logit function and \(p\) is the probability of incidence of diabetes mellitus.
The fitted coefficients and knot locations are given in the following tables.
Table 45: Diabetes Incidence
Table 46: Diabetes Delta BMI Knots
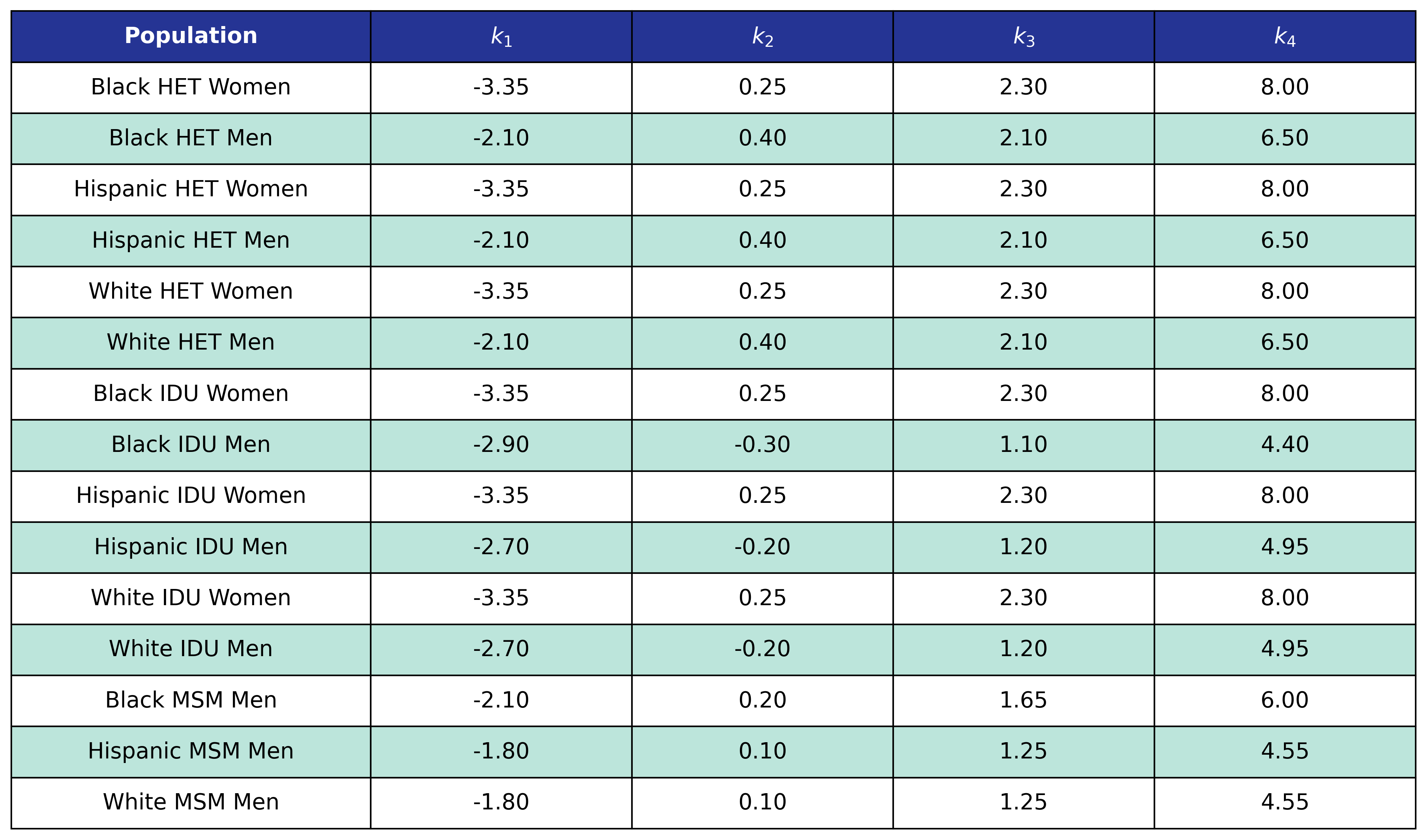
Table 47: Diabetes Post-ART BMI Knots
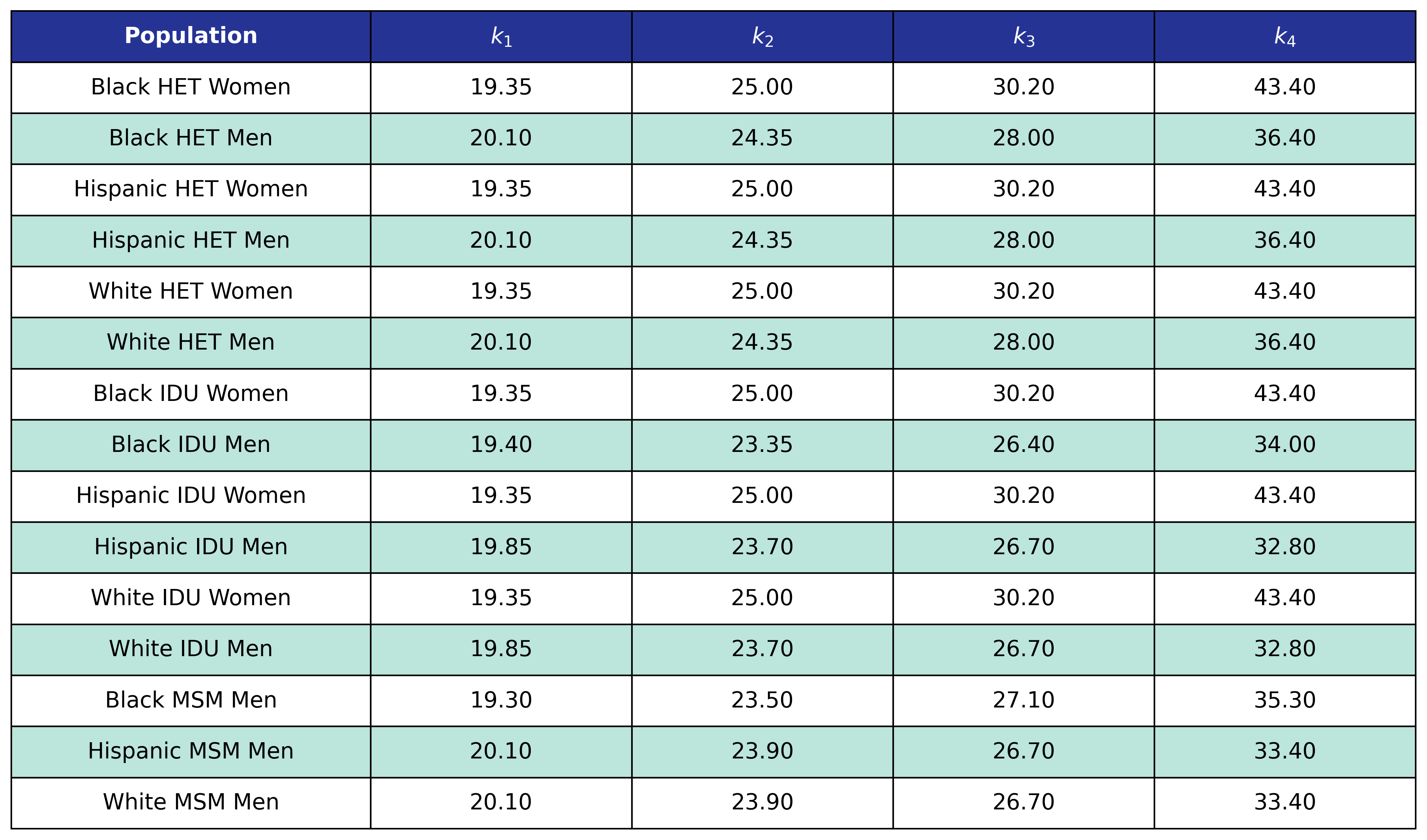
Hypertension
At the beginning of the simulation each member of the initial population begins with \(\mathrm{hypertension} = 1\) with probability given by the first column in the table. At the start of each year new ART initiators are added where \(\mathrm{hypertension} = 1\) with probability given by the second column in the table.
Table 48: Hypertension Prevalence
At the beginning of each year the in care and out of care populations with \(\mathrm{hypertension} = 0\) have probability for incidence of hypertension given by
\[\begin{split} \mathrm{logit}(p) = \beta_0 &+ \beta_\mathrm{year}\cdot\mathrm{year} + \beta_\mathrm{age}\cdot\mathrm{age} + \beta_\mathrm{sqrt\_init\_cd4}\cdot\mathrm{sqrt\_init\_cd4} + \beta_\mathrm{time\_since\_art} \cdot \mathrm{time\_since\_art} \\[2ex] &+ \beta_\mathrm{delta\_bmi} \cdot \mathrm{delta\_bmi} + \beta_\mathrm{delta\_bmi\_1} \cdot \mathrm{delta\_bmi\_1} + \beta_\mathrm{delta\_bmi\_2} \cdot \mathrm{delta\_bmi\_2} \\[2ex] &+ \beta_\mathrm{post\_art\_bmi} \cdot \mathrm{post\_art\_bmi} + \beta_\mathrm{post\_art\_bmi\_1} \cdot \mathrm{post\_art\_bmi\_1} + \beta_\mathrm{post\_art\_bmi\_2} \cdot \mathrm{post\_art\_bmi\_2} \\[2ex] &+ \beta_\mathrm{smoking} \cdot \mathrm{smoking} + \beta_\mathrm{hcv} \cdot \mathrm{hcv} + \beta_\mathrm{anxiety} \cdot \mathrm{anxiety} + \beta_\mathrm{depression} \cdot \mathrm{depression} \\[2ex] &+ \beta_\mathrm{ckd} \cdot \mathrm{ckd} + \beta_\mathrm{lipid} \cdot \mathrm{lipid} + \beta_\mathrm{diabetes} \cdot \mathrm{diabetes} \end{split}\]where
\[\mathrm{logit}(p) = \log \frac{p}{1 - p}\]is the logit function and \(p\) is the probability of incidence of hypertension.
The fitted coefficients and knot locations are given in the following tables.
Table 49: Hypertension Incidence
Table 50: Hypertension Delta BMI Knots
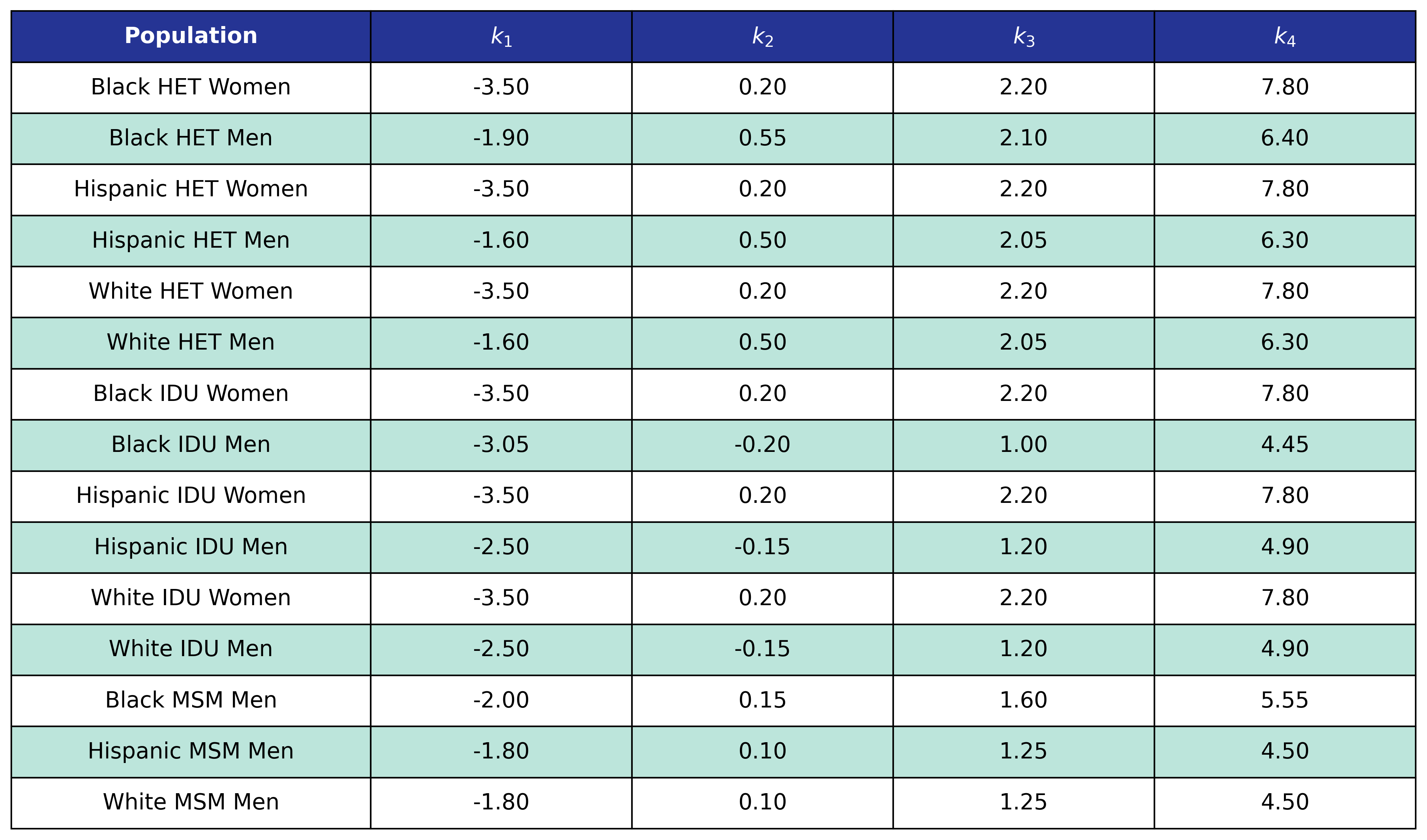
Table 51: Hypertension Post-ART BMI Knots
Stage 3
The stage 3 conditions are cancer, end-stage liver disease (ELSD), and myocardial infarction (MI). Prevalence in the 2009 ART user population is taken from the 2009 NA-ACCORD population, while prevalence in ART initiators was taken from the 2009 - 2017 NA-ACCORD ART initiator population. Incidence is modeled using logistic regression and is based on NA-ACCORD data. The logistic regression models the logit of probability for incidence of a stage 3 condition as a linear function of calendar year (\(\mathrm{year}\)), age (\(\mathrm{age}\)), square root of CD4 count at ART initiation (\(\mathrm{sqrt\_init\_cd4}\)), number of years since ART initiation (\(\mathrm{time\_since\_art}\)), change in BMI after ART initiation (\(\mathrm{delta\_bmi}\)) and BMI after ART initiation (\(\mathrm{post\_art\_bmi}\)) modeled as restricted cubic splines, stage 0 condition status (\(\mathrm{smoking}\), \(\mathrm{hcv}\)), stage 1 condition status (\(\mathrm{anxiety}\), \(\mathrm{depression}\)), and stage 2 condition status (\(\mathrm{ckd}\), \(\mathrm{lipid}\), \(\mathrm{diabetes}\), \(\mathrm{hypertension}\)).
At the beginning of the simulation each member of the initial population begins with \(\mathrm{stage\_3} = 1\) with probability given by the first column in the table. At the start of each year new ART initiators are added where \(\mathrm{stage\_3} = 1\) with probability given by the second column in the table. Here \(\mathrm{stage\_3}\) are \(\mathrm{cancer}\), \(\mathrm{esld}\), and \(\mathrm{mi}\). These prevalences are:
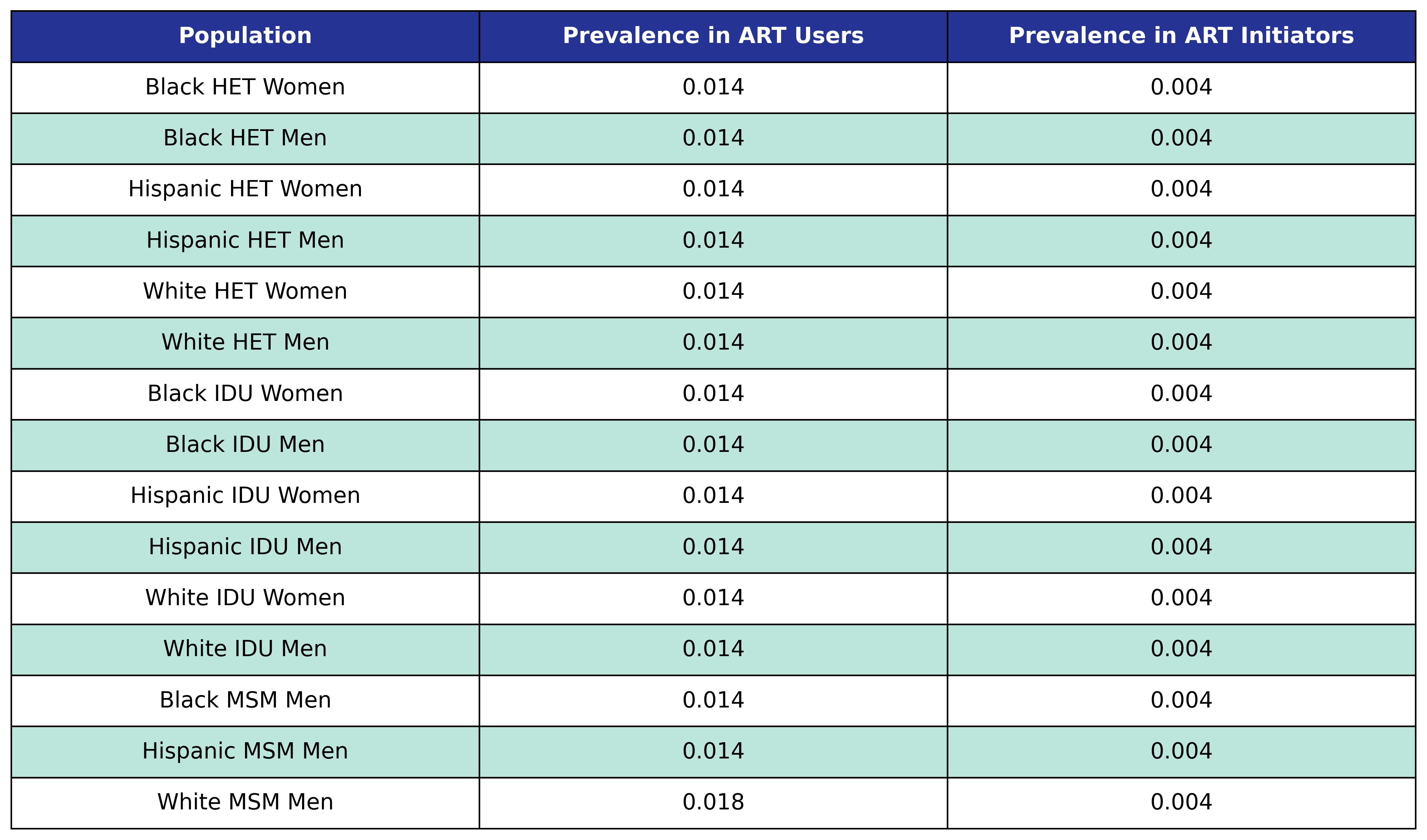
Table 52: Cancer Prevalence
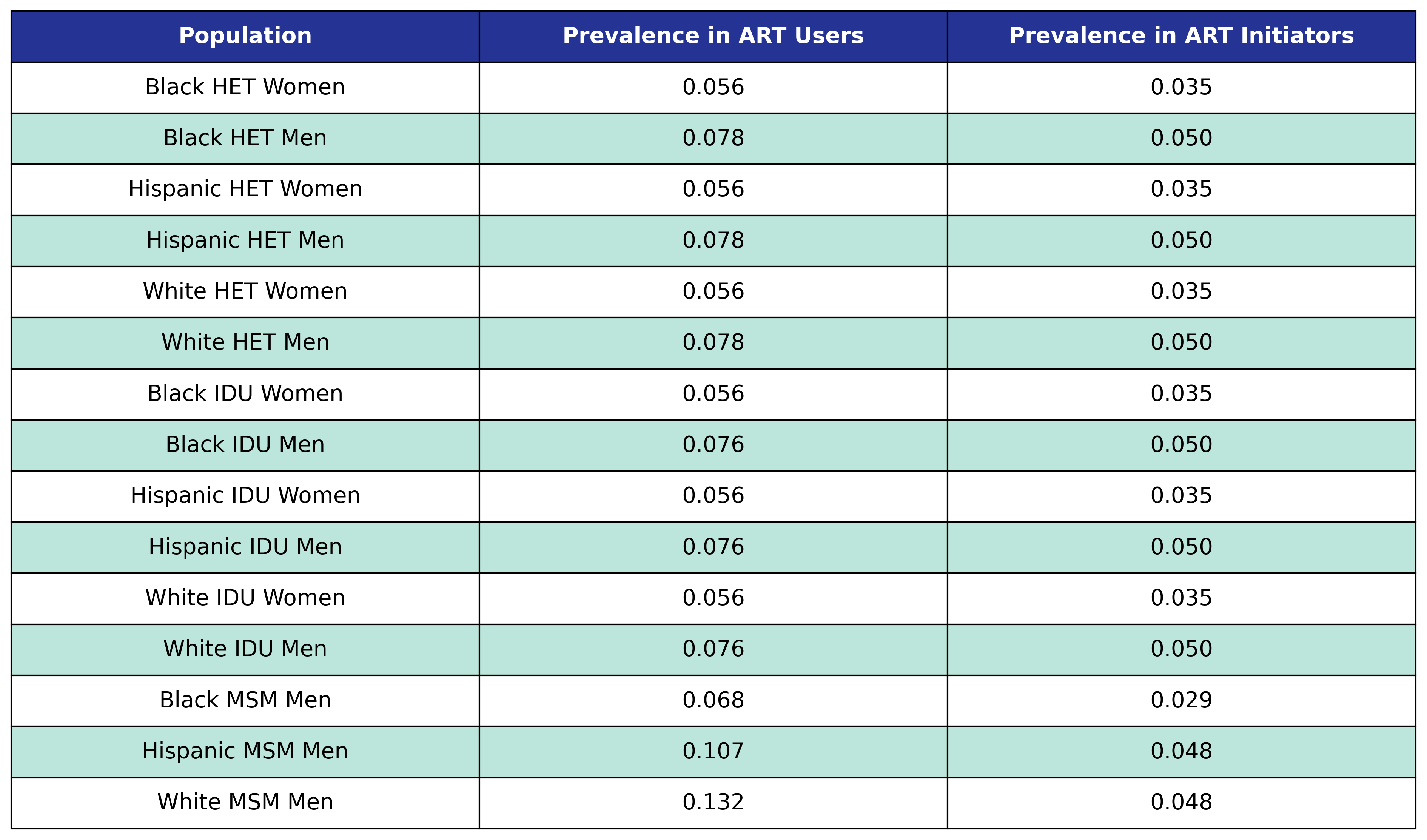
Table 53: ESLD Prevalence
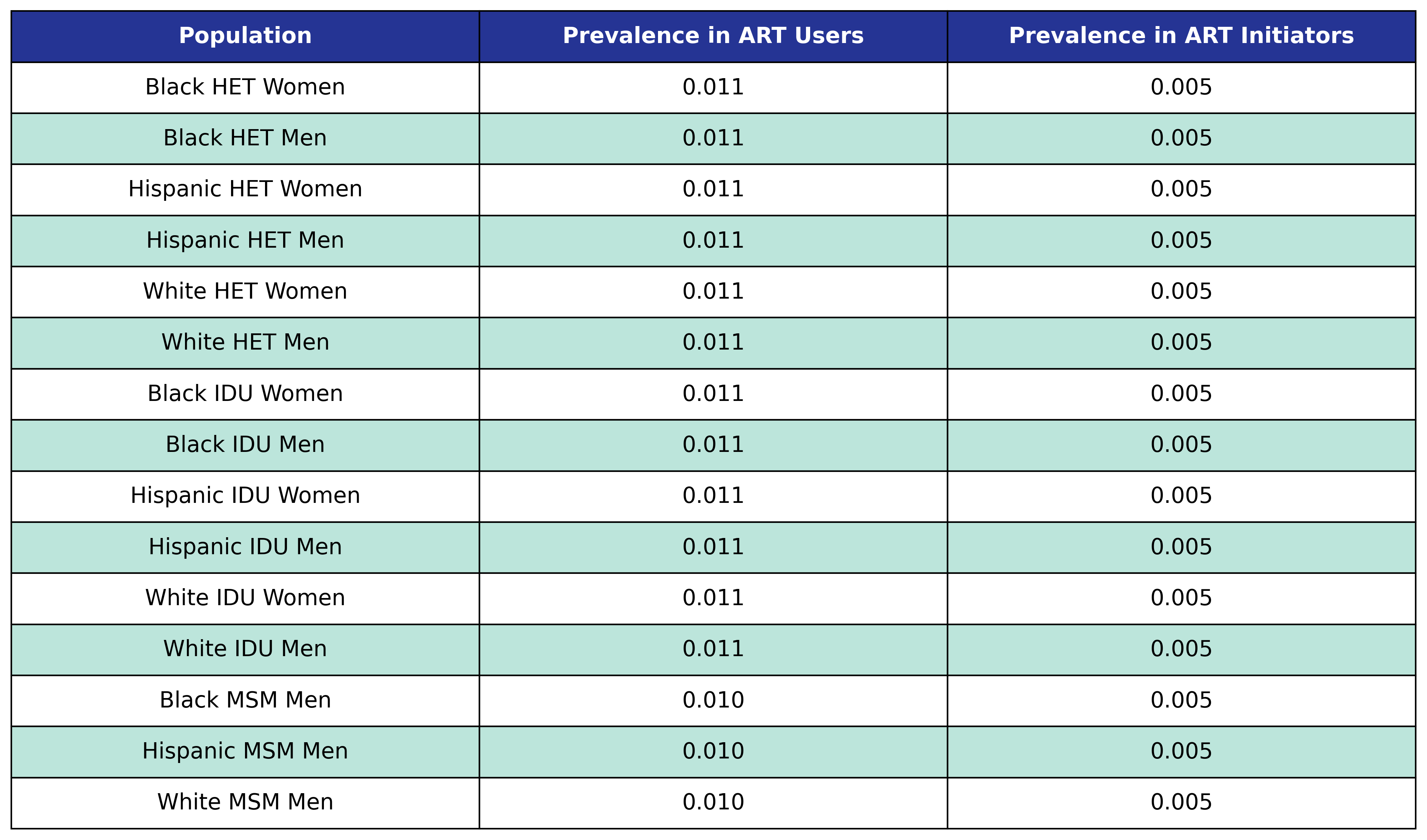
Table 54: MI Prevalence
All three stage 3 comorbidities use the same incidence probability function given by
\[\begin{split} \mathrm{logit}(p) = \beta_0 &+ \beta_\mathrm{year}\cdot\mathrm{year} + \beta_\mathrm{age}\cdot\mathrm{age} + \beta_\mathrm{sqrt\_init\_cd4}\cdot\mathrm{sqrt\_init\_cd4} + \beta_\mathrm{time\_since\_art} \cdot \mathrm{time\_since\_art} \\[2ex] &+ \beta_\mathrm{delta\_bmi} \cdot \mathrm{delta\_bmi} + \beta_\mathrm{delta\_bmi\_1} \cdot \mathrm{delta\_bmi\_1} + \beta_\mathrm{delta\_bmi\_2} \cdot \mathrm{delta\_bmi\_2} \\[2ex] &+ \beta_\mathrm{post\_art\_bmi} \cdot \mathrm{post\_art\_bmi} + \beta_\mathrm{post\_art\_bmi\_1} \cdot \mathrm{post\_art\_bmi\_1} + \beta_\mathrm{post\_art\_bmi\_2} \cdot \mathrm{post\_art\_bmi\_2} \\[2ex] &+ \beta_\mathrm{smoking} \cdot \mathrm{smoking} + \beta_\mathrm{hcv} \cdot \mathrm{hcv} + \beta_\mathrm{anxiety} \cdot \mathrm{anxiety} + \beta_\mathrm{depression} \cdot \mathrm{depression} \\[2ex] &+ \beta_\mathrm{ckd} \cdot \mathrm{ckd} + \beta_\mathrm{lipid} \cdot \mathrm{lipid} + \beta_\mathrm{diabetes} \cdot \mathrm{diabetes} +\beta_\mathrm{hypertension} \cdot \mathrm{hypertension}. \end{split}\]The fitted coefficients and knot locations are given in the following tables.
Table 55: Cancer Incidence
Table 56: Cancer Delta BMI Knots
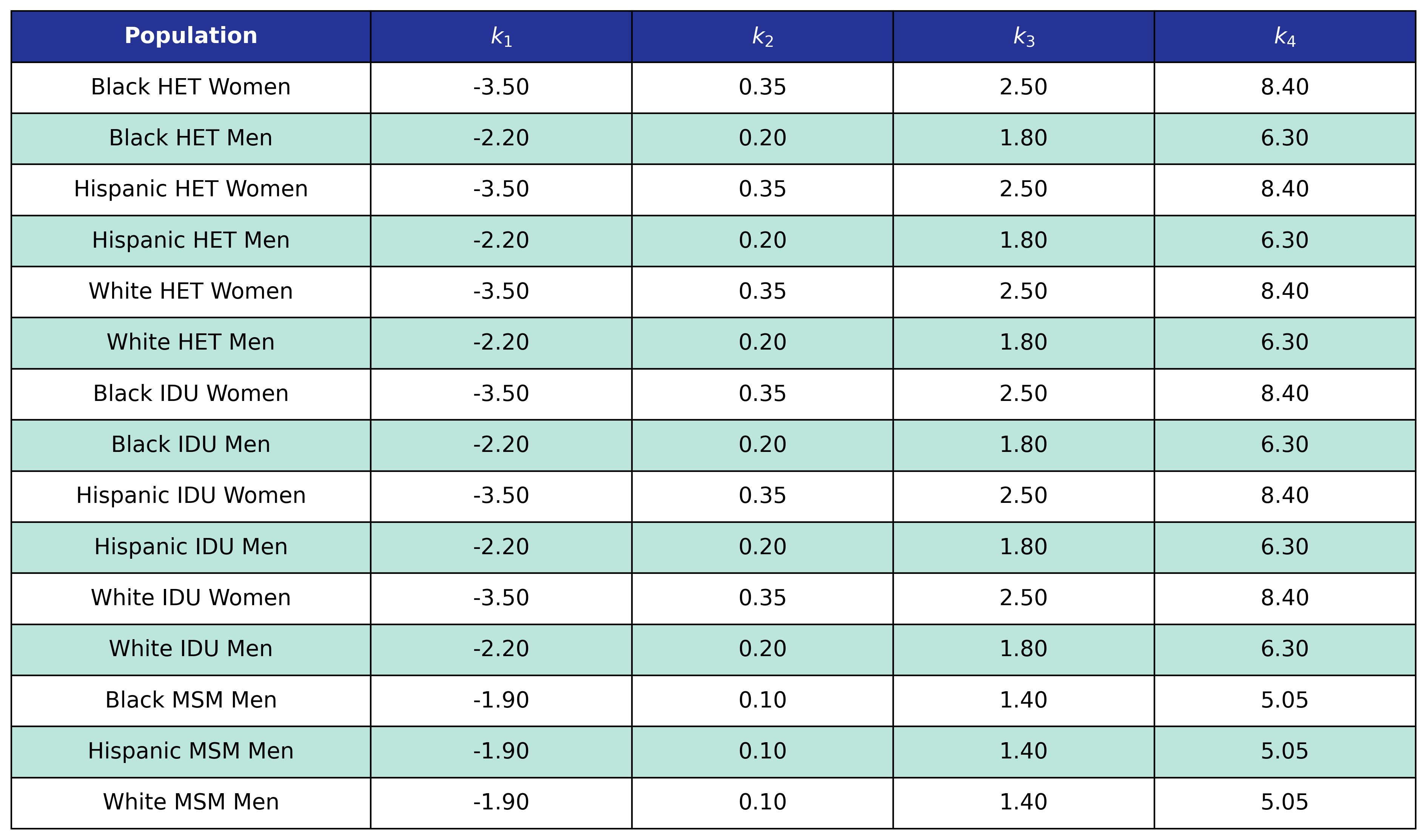
Table 57: Cancer Post-ART BMI Knots
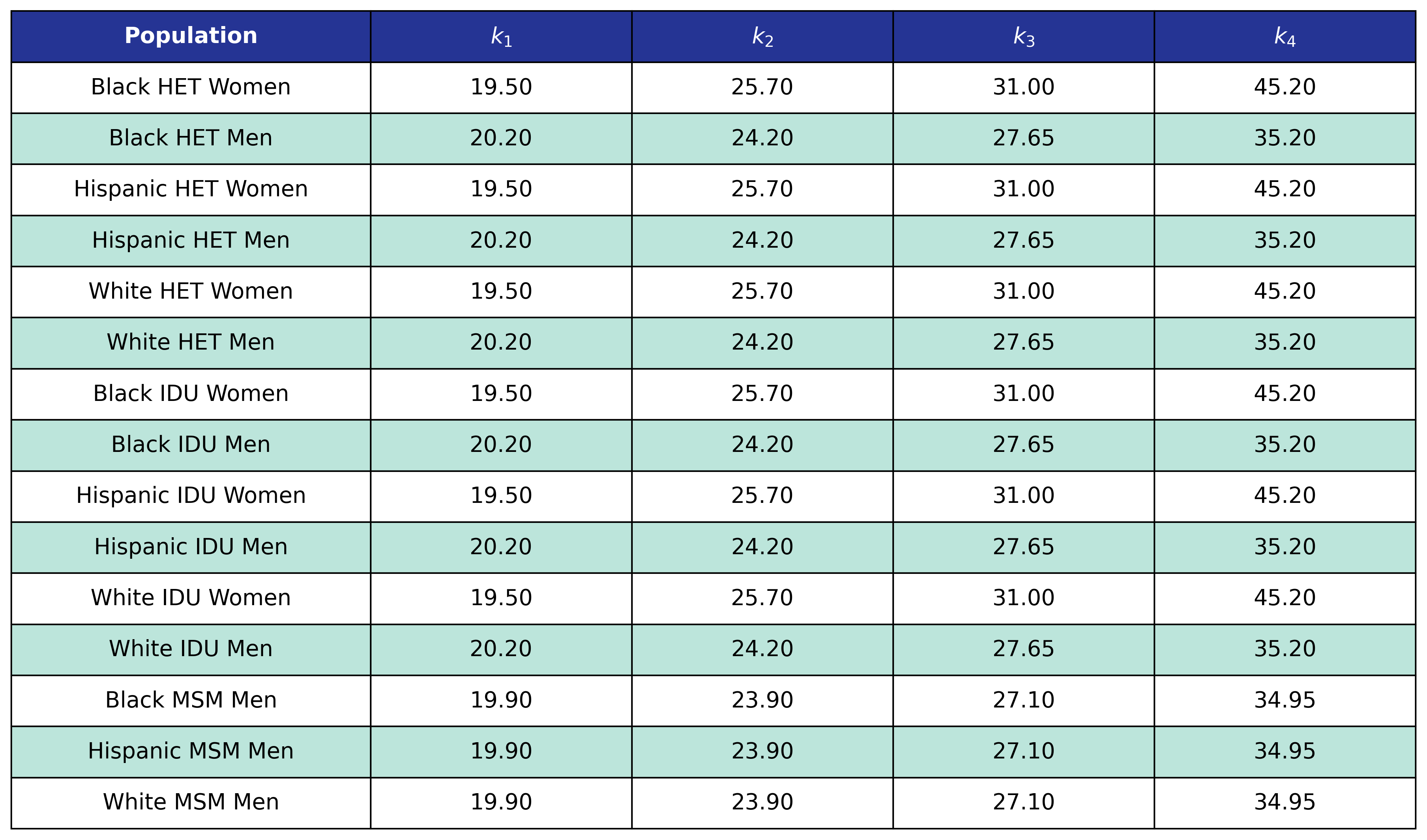
Table 58: ESLD Incidence
Table 59: ESLD Delta BMI Knots
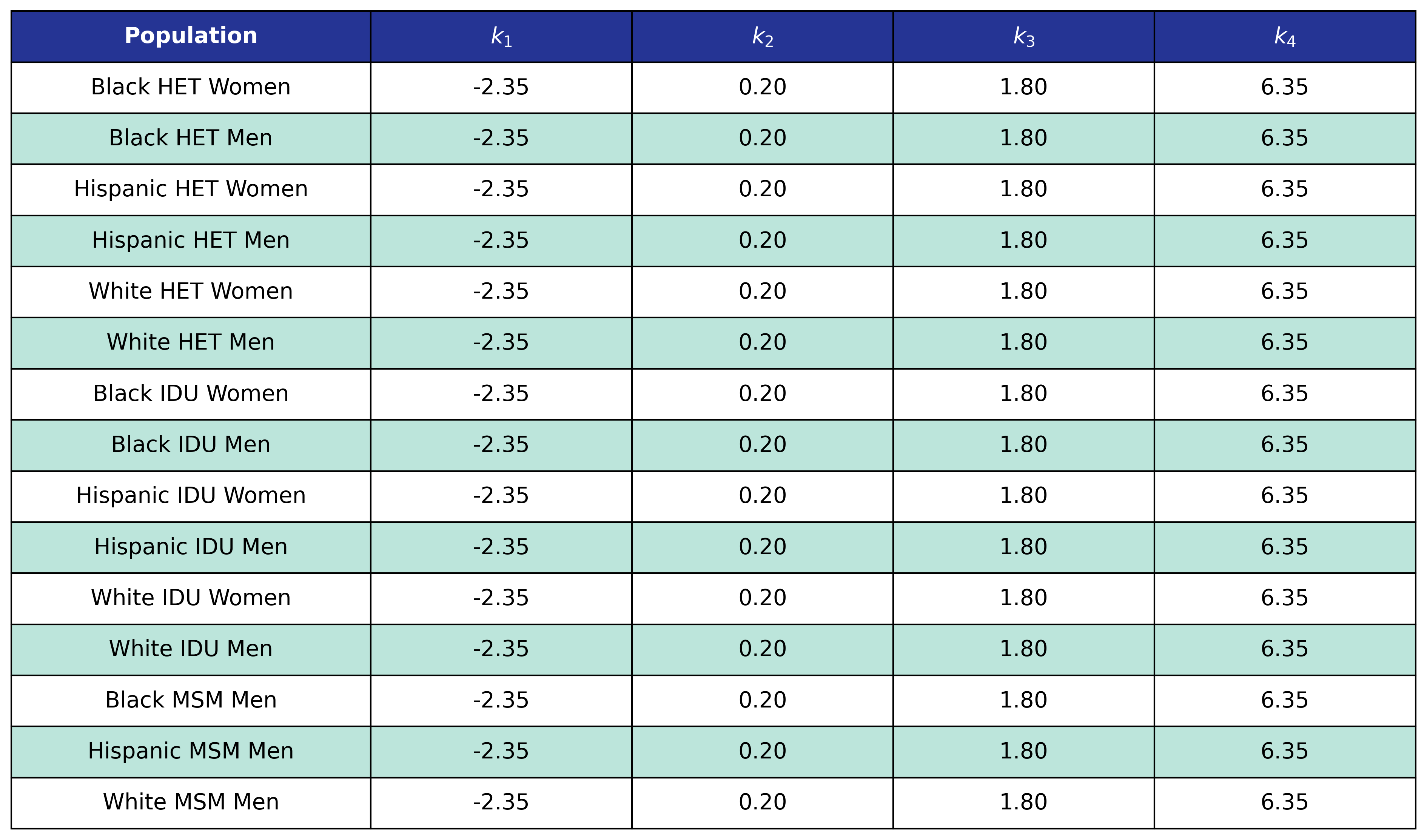
Table 60: ESLD Post-ART BMI Knots
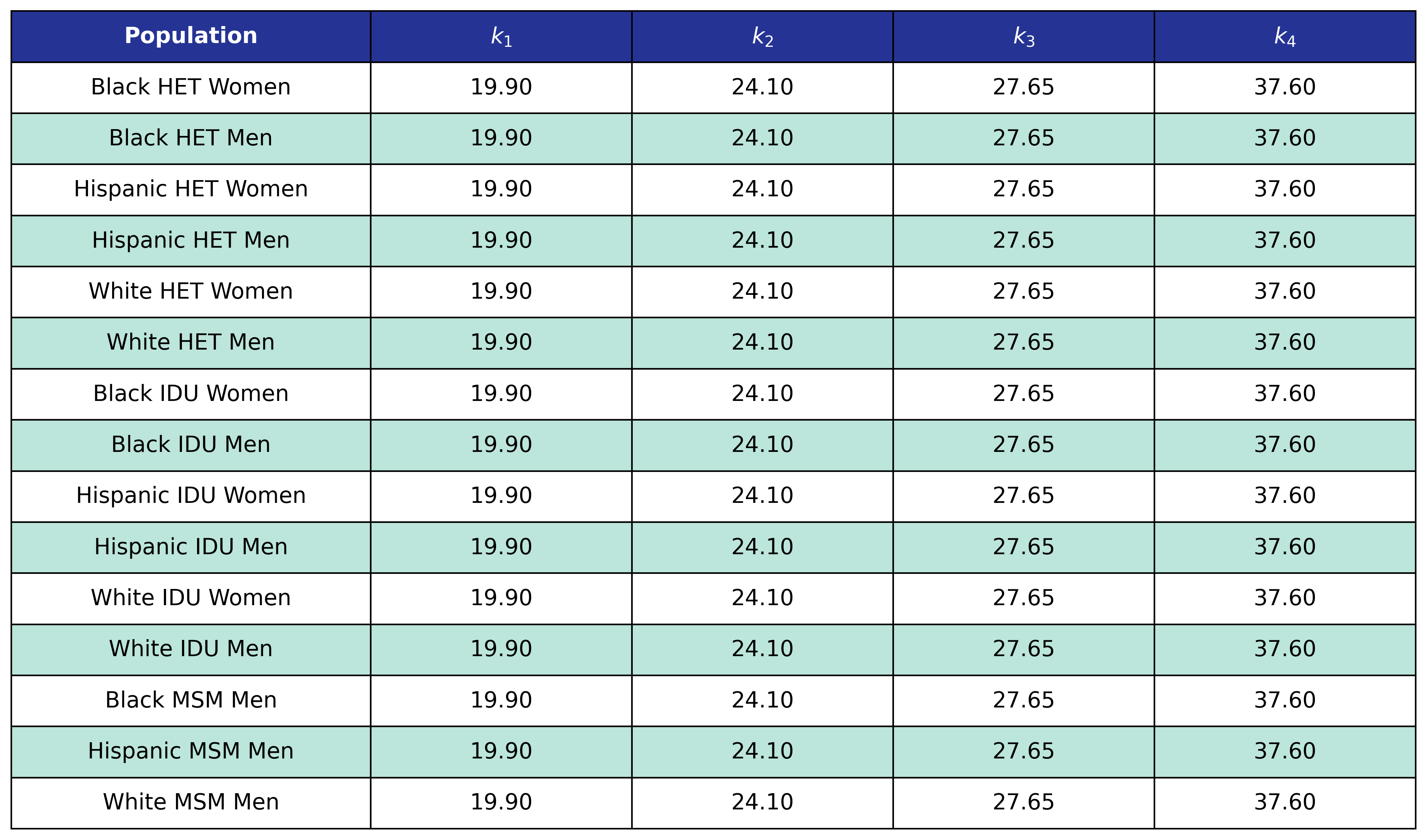
Table 61: MI Incidence
Table 62: MI Delta BMI Knots
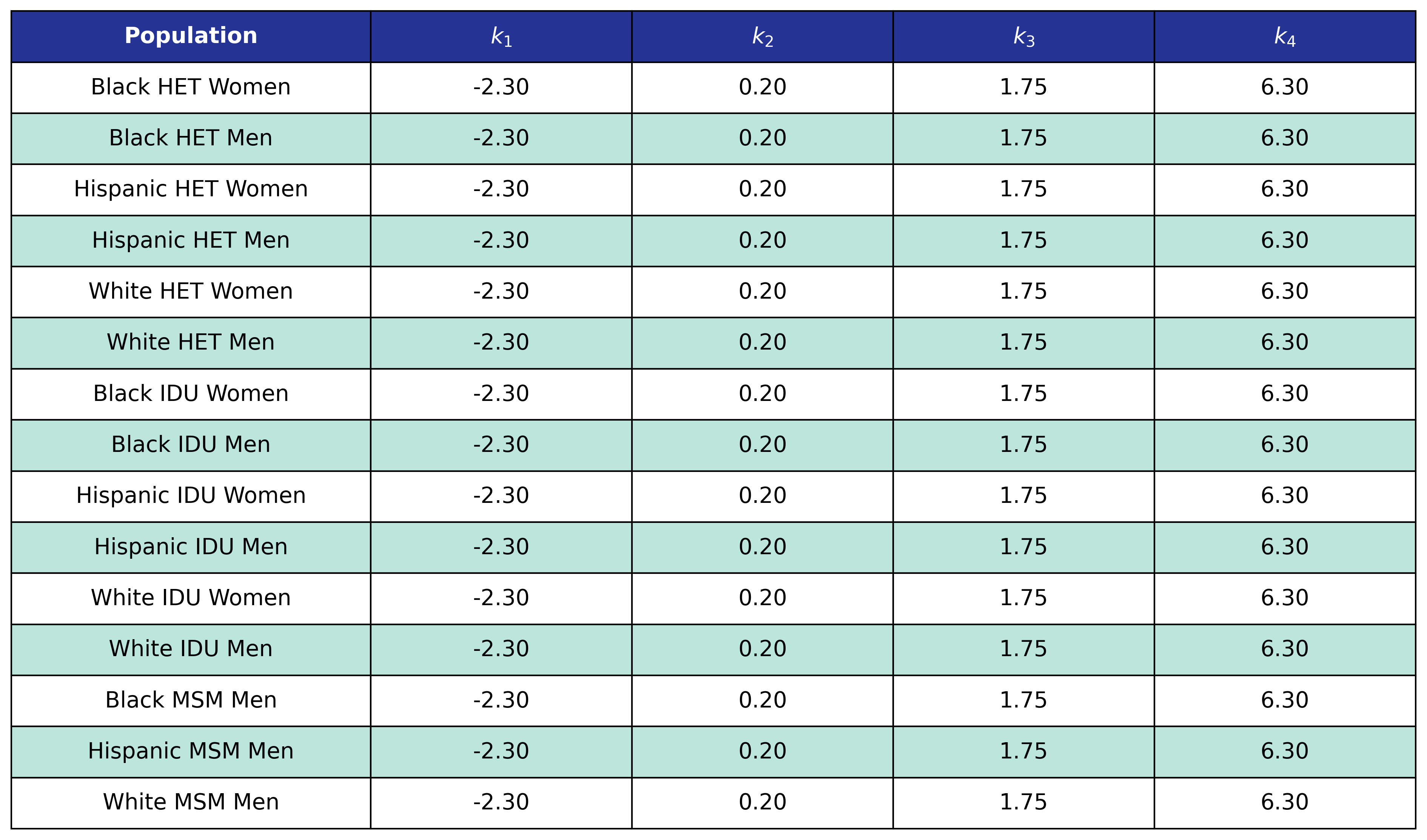
Table 63: MI Post-ART BMI Knots
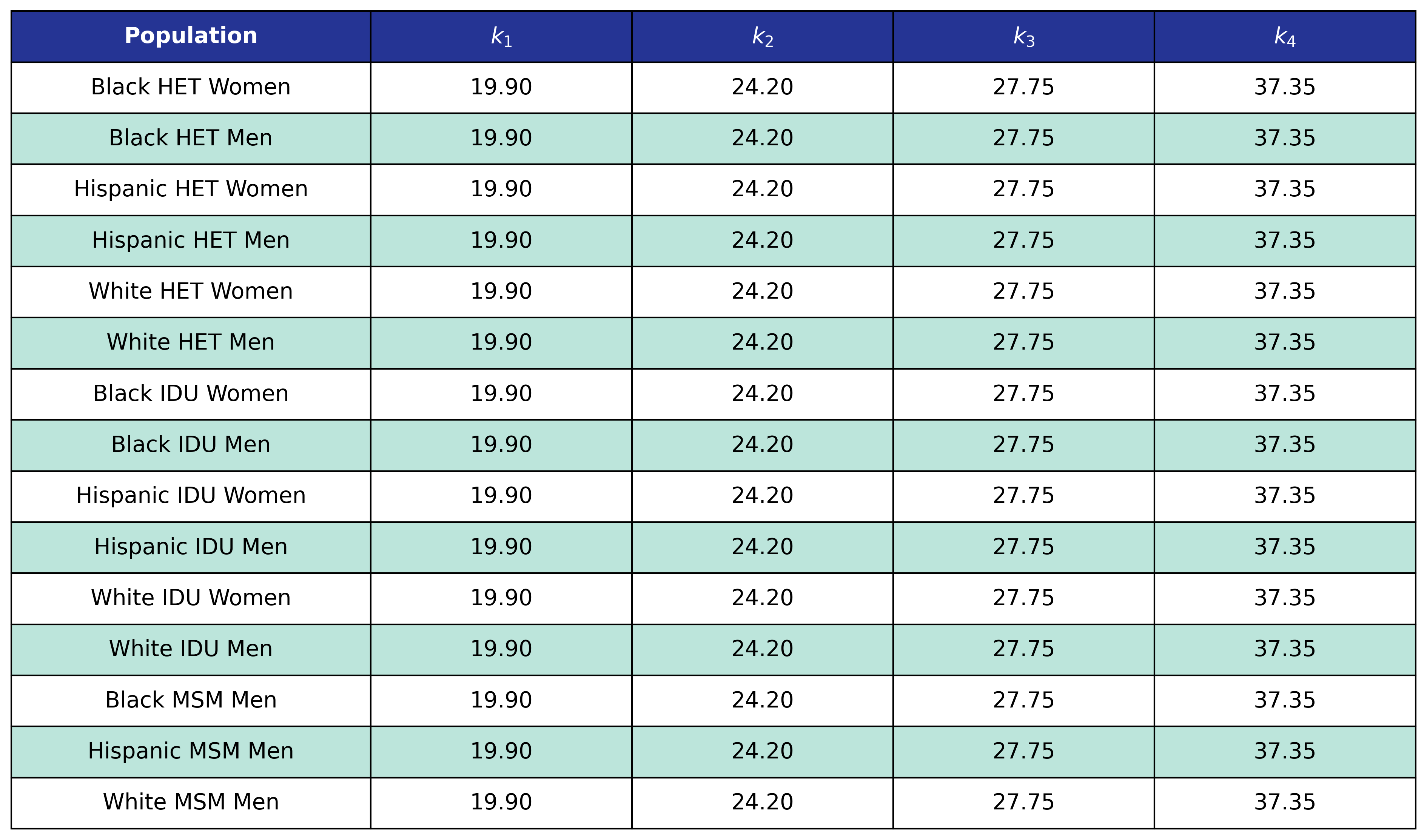
Modified Mortality Functions with Comorbidities
The mortality functions are modified to include all stages of comorbidity.
Mortality In Care
We use logistic regression to model the probability of dying in care as a function of calendar year (\(\mathrm{year}\)), 10 year age category (\(\mathrm{age\_cat}\)), CD4 count at ART initiation (\(\mathrm{sqrt\_init\_cd4}\)), year of ART initiation (\(\mathrm{art\_init\_year}\)), BMI after ART initiation (\(\mathrm{post\_art\_bmi}\)) modeled as a restricted cubic spline, stage 0 comorbiditities (\(\mathrm{smoking}\), \(\mathrm{hcv}\)), stage 1 comorbidities (\(\mathrm{anxiety}\), \(\mathrm{depression}\)), stage 2 comorbiditities (\(\mathrm{ckd}\), \(\mathrm{lipid}\), \(\mathrm{diabetes}\), \(\mathrm{hypertension}\)), and stage 3 comorbidities (\(\mathrm{cancer}\), \(\mathrm{esld}\), \(\mathrm{mi}\)).
\[\begin{split} \mathrm{logit}(p) = \beta_0 &+\beta_\mathrm{year}\cdot\mathrm{year}+\beta_\mathrm{age\_cat}\cdot\mathrm{age\_cat}+\beta_\mathrm{sqrt\_init\_cd4}\cdot\mathrm{sqrt\_init\_cd4}+\beta_\mathrm{art\_init\_year}\cdot\mathrm{art\_init\_year}\\[2ex] &+ \beta_\mathrm{post\_art\_bmi} \cdot \mathrm{post\_art\_bmi} + \beta_\mathrm{post\_art\_bmi\_1} \cdot \mathrm{post\_art\_bmi\_1}+ \beta_\mathrm{post\_art\_bmi\_2} \cdot \mathrm{post\_art\_bmi\_2}\\[2ex] &+\beta_\mathrm{smoking} \cdot\mathrm{smoking}+\beta_\mathrm{hcv}\cdot\mathrm{hcv}+\beta_\mathrm{anxiety}\cdot\mathrm{anxiety}+\beta_\mathrm{depression}\cdot\mathrm{depression}+\beta_\mathrm{ckd}\cdot\mathrm{ckd}\\[2ex] &+\beta_\mathrm{lipid}\cdot\mathrm{lipid} + \beta_\mathrm{diabetes} \cdot\mathrm{diabetes} + \beta_\mathrm{hypertension} \cdot\mathrm{hypertension}+\beta_\mathrm{cancer} \cdot\mathrm{cancer}+\beta_\mathrm{esld} \cdot\mathrm{esld}+\beta_\mathrm{mi} \cdot\mathrm{mi} \end{split}\]where
\[\mathrm{logit}(p) = \log \frac{p}{1 - p}\]is the logit function and \(p\) is probability of dying in care. The coefficients were estimated using a Generalized Estimating Equation (GEE) with a logit link and an unstructured correlation structure using the geepack software package for R. The NA-ACCORD dataset was restricted to the years 2009-2015 and each patient is represented by a data point for each year they were alive and under observation in NA-ACCORD. The regression resulted in the following coefficient estimates and knots:
Table 64: Mortality In Care Coefficient Estimates
Table 65: Mortality In Care Post-ART BMI Knots
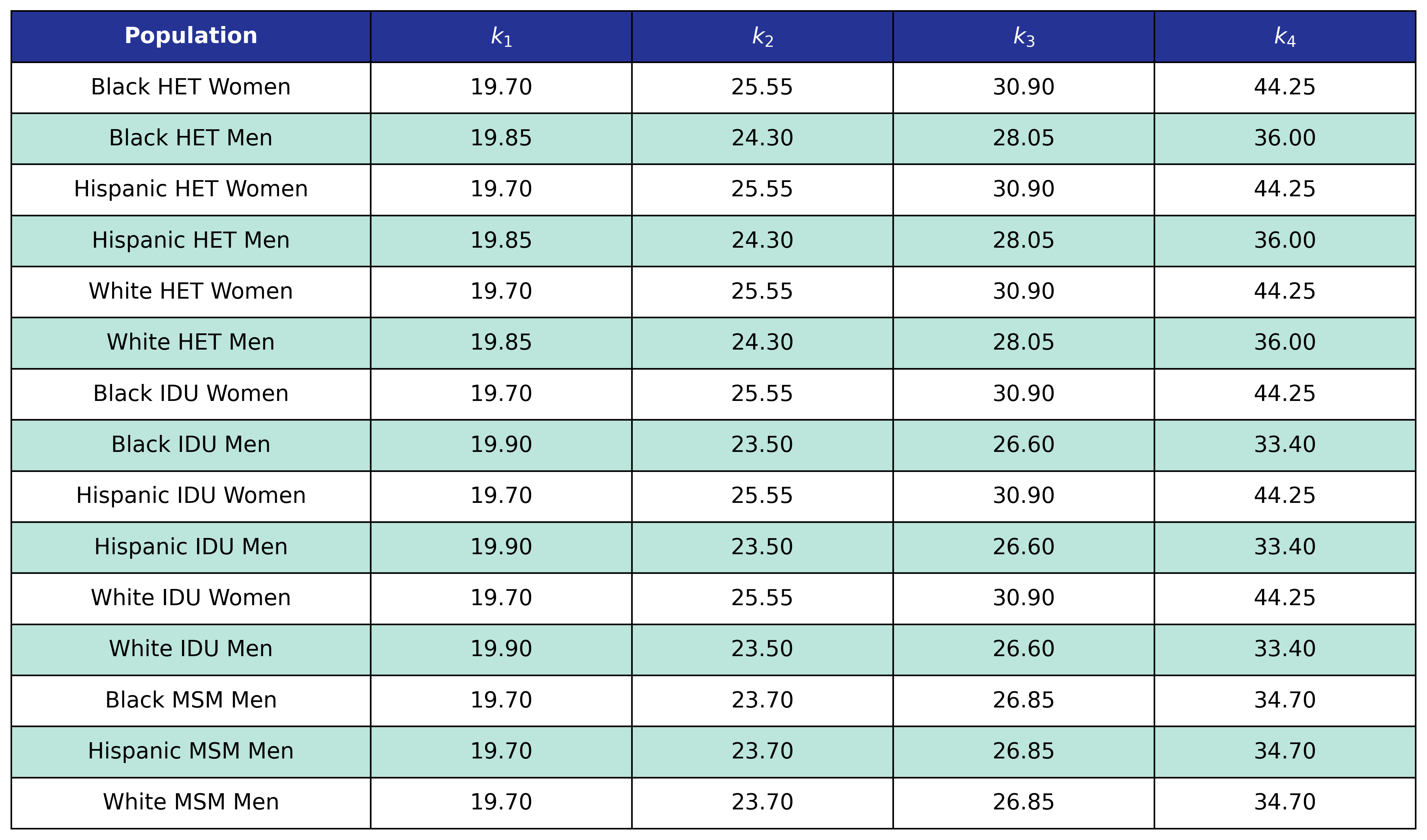
Mortality Out of Care
We use logistic regression to model the probability of dying in care as a function of calendar year (\(\mathrm{year}\)), 10 year age category (\(\mathrm{age\_cat}\)), CD4 count(\(\mathrm{sqrt\_cd4}\)), BMI after ART initiation (\(\mathrm{post\_art\_bmi}\)) modeled as a restricted cubic spline, stage 0 comorbidities (\(\mathrm{smoking}\), \(\mathrm{hcv}\)), stage 1 comorbidities (\(\mathrm{anxiety}\), \(\mathrm{depression}\)), stage 2 comorbiditities (\(\mathrm{ckd}\), \(\mathrm{lipid}\), \(\mathrm{diabetes}\), \(\mathrm{hypertension}\)), and stage 3 comorbidities (\(\mathrm{cancer}\), \(\mathrm{esld}\), \(\mathrm{mi}\)).
\[\begin{split} \mathrm{logit}(p) = \beta_0 &+\beta_\mathrm{year}\cdot\mathrm{year}+\beta_\mathrm{age\_cat}\cdot\mathrm{age\_cat}+\beta_\mathrm{sqrt\_cd4}\cdot\mathrm{sqrt\_cd4} + \beta_\mathrm{post\_art\_bmi} \cdot \mathrm{post\_art\_bmi}\\[2ex] &+ \beta_\mathrm{post\_art\_bmi\_1} \cdot \mathrm{post\_art\_bmi\_1}+ \beta_\mathrm{post\_art\_bmi\_2} \cdot \mathrm{post\_art\_bmi\_2} +\beta_\mathrm{smoking} \cdot\mathrm{smoking}\\[2ex] &+\beta_\mathrm{hcv}\cdot\mathrm{hcv}+\beta_\mathrm{anxiety}\cdot\mathrm{anxiety}+\beta_\mathrm{depression}\cdot\mathrm{depression}+\beta_\mathrm{ckd}\cdot\mathrm{ckd} +\beta_\mathrm{lipid}\cdot\mathrm{lipid}\\[2ex] &+ \beta_\mathrm{diabetes} \cdot\mathrm{diabetes}+ \beta_\mathrm{hypertension} \cdot\mathrm{hypertension}+\beta_\mathrm{cancer} \cdot\mathrm{cancer}+\beta_\mathrm{esld} \cdot\mathrm{esld}+\beta_\mathrm{mi} \cdot\mathrm{mi} \end{split}\]where
\[\mathrm{logit}(p) = \log \frac{p}{1 - p}\]is the logit function and \(p\) is the probability of dying out of care. The coefficients were estimated using a Generalized Estimating Equation (GEE) with a logit link and an unstructured correlation structure using the geepack software package for R. The NA-ACCORD dataset was restricted to the years 2009-2015 and each patient was represented by a data point for each year they were alive and under observation in NA-ACCORD. The regression resulted in the following coefficient estimates and knots:
Table 66: Mortality Out Of Care Coefficient Estimates
Table 67: Mortality Out Of Care Post-ART BMI Knots
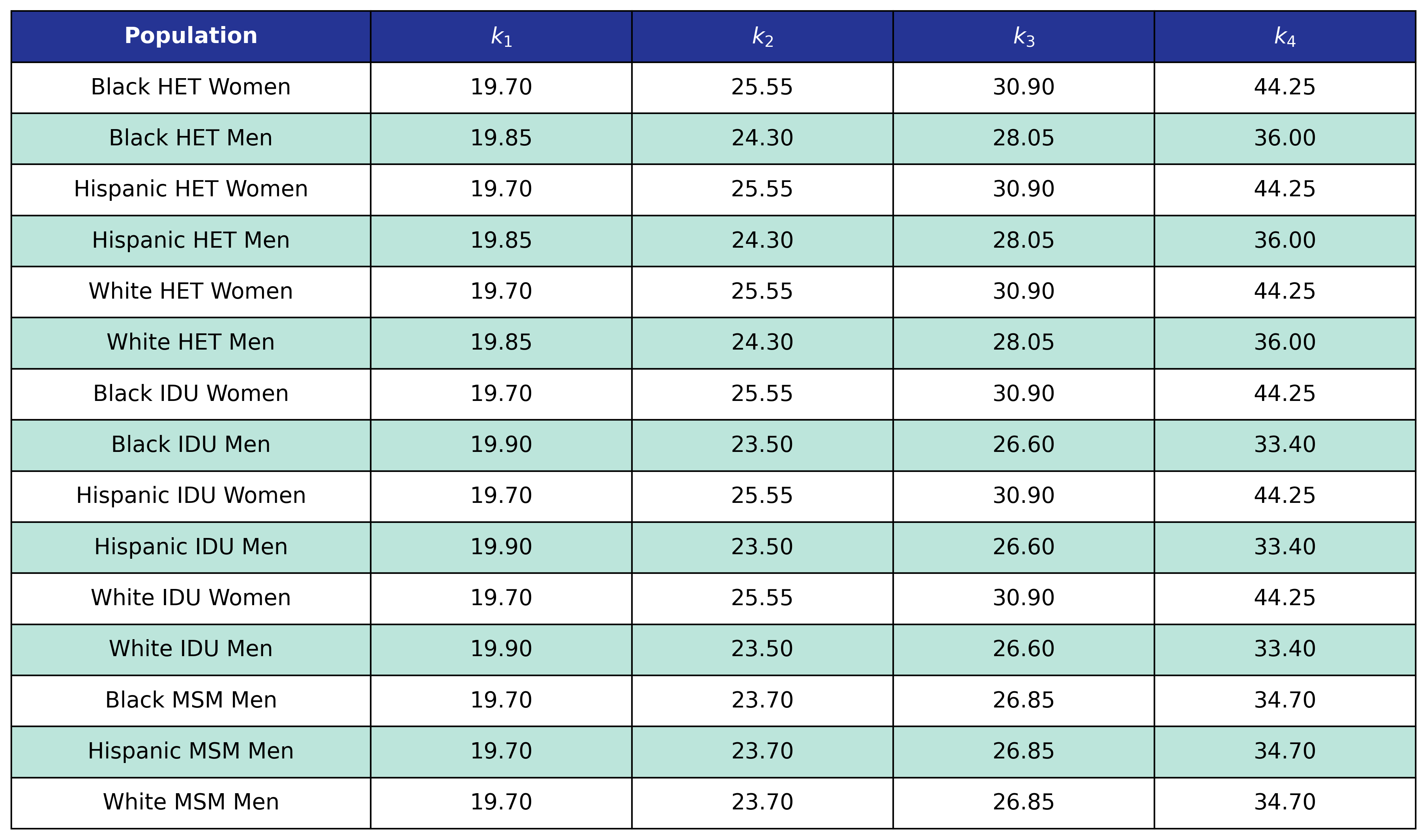
Restricted Cubic Spline
Many functions in PEARL model variables using a restricted cubic spline. These spline variables are defined as
\[x\_1 = \max{\left( 0, \frac{x - k_1}{k_\mathrm{norm}}\right) }^3 - \left( \frac{k_4 - k_1}{k_4 - k_3}\right) \cdot \max{\left( 0, \frac{x - k_3}{k_\mathrm{norm}}\right) } ^3 + \left( \frac{k_3 - k_1}{k_4 - k_3}\right) \cdot \max{\left( 0, \frac{x - k_4}{k_\mathrm{norm}}\right) } ^3\]and
\[x\_2 = \max{\left( 0, \frac{x - k_2}{k_\mathrm{norm}}\right) }^3 - \left( \frac{k_4 - k_2}{k_4 - k_3}\right) \cdot \max{\left( 0, \frac{x - k_3}{k_\mathrm{norm}}\right) } ^3 + \left( \frac{k_3 - k_2}{k_4 - k_3}\right) \cdot \max{\left( 0, \frac{x - k_4}{k_\mathrm{norm}}\right) } ^3\]where \(k\) are the knot locations and
\[k_\mathrm{norm} = \left( k_4 - k_1 \right)^\frac{2}{3}\]is a normalization factor.